题目内容
若x≥0,y≥0,且x+2y=1,那么2x+y2的最小值为
- A.

- B.-2
- C.

- D.2
C
分析:先将二元转化为一元,再利用配方法求函数的最小值,即可得到结论.
解答:∵x+2y=1,∴x=1-2y,
∴2x+y2=y2-4y+2=(y-2)2-2
∵x≥0,∴1-2y≥0,∴0≤y≤
∴函数在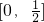 上单调递减
上单调递减
∴y= 时,2x+y2的最小值为
时,2x+y2的最小值为
故选C.
点评:本题考查二次函数在指定区间上的最值,考查学生分析解决问题的能力,确定二次函数是关键.
分析:先将二元转化为一元,再利用配方法求函数的最小值,即可得到结论.
解答:∵x+2y=1,∴x=1-2y,
∴2x+y2=y2-4y+2=(y-2)2-2
∵x≥0,∴1-2y≥0,∴0≤y≤

∴函数在
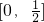 上单调递减
上单调递减∴y=
 时,2x+y2的最小值为
时,2x+y2的最小值为
故选C.
点评:本题考查二次函数在指定区间上的最值,考查学生分析解决问题的能力,确定二次函数是关键.

练习册系列答案
相关题目