题目内容
若函数y=f(x)(x∈R+)同时满足:①对一切正数x都有f(3x)=3f(x),②f(x)=1-|x-2|(1≤x≤3),则f(100)=则方程f(x)=f(100)的解的最小值为________.
46
分析:f(100)=3f( )=3f(3×
)=3f(3× )=9f(
)=9f( )=…=81f(
)=…=81f( ),由此猜想f(x)=
),由此猜想f(x)= ,由
,由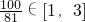 ,知
,知 =81•[1-|
=81•[1-|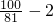 |]=19,f(100)=19,由此能求出方程f(x)=f(100)解的最小值.
|]=19,f(100)=19,由此能求出方程f(x)=f(100)解的最小值.
解答:f(100)=3f( )=3f(3×
)=3f(3× )=9f(
)=9f( )=…=81f(
)=…=81f( ),
),
由此猜想f(x)= ,
,
∵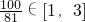 ,∴
,∴ =81•[1-|
=81•[1-|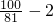 |]=19,
|]=19,
∴f(100)=19,
由f(x)=19,知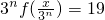 ,
,
当1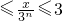 ,即3n≤x≤3n+1时,
,即3n≤x≤3n+1时,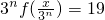 可化为
可化为 ,
,
即3n-|2•3n-x|=19,x=19+3n,或x=3n+1-19,
又3n≤x≤3n+1,则n≥3,
当n=3时,x=19+27=46,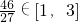 ,或x=62,
,或x=62,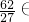 [1,3],
[1,3],
故方程f(x)=f(100)解的最小值为46.
点评:本题考查归纳推理的应用,解题时要认真审题,仔细解答,注意抽象函数的性质及其应用.
分析:f(100)=3f(
 )=3f(3×
)=3f(3× )=9f(
)=9f( )=…=81f(
)=…=81f( ),由此猜想f(x)=
),由此猜想f(x)= ,由
,由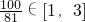 ,知
,知 =81•[1-|
=81•[1-|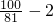 |]=19,f(100)=19,由此能求出方程f(x)=f(100)解的最小值.
|]=19,f(100)=19,由此能求出方程f(x)=f(100)解的最小值.解答:f(100)=3f(
 )=3f(3×
)=3f(3× )=9f(
)=9f( )=…=81f(
)=…=81f( ),
),由此猜想f(x)=
 ,
,∵
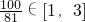 ,∴
,∴ =81•[1-|
=81•[1-|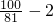 |]=19,
|]=19,∴f(100)=19,
由f(x)=19,知
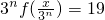 ,
,当1
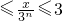 ,即3n≤x≤3n+1时,
,即3n≤x≤3n+1时,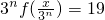 可化为
可化为 ,
,即3n-|2•3n-x|=19,x=19+3n,或x=3n+1-19,
又3n≤x≤3n+1,则n≥3,
当n=3时,x=19+27=46,
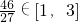 ,或x=62,
,或x=62,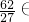 [1,3],
[1,3],故方程f(x)=f(100)解的最小值为46.
点评:本题考查归纳推理的应用,解题时要认真审题,仔细解答,注意抽象函数的性质及其应用.

练习册系列答案
相关题目