题目内容
二次函数的图象过点(-2,1),且在[1,+∞)上是减少的,则这个函数的解析式可以为
y=-x2+2x+9
y=-x2+2x+9
.分析:先设出函数解析式y=ax2+bx+c(a≠0),由图象过点(-2,1)得一方程,根据函数在[1,+∞)上递减,得a<0,及对称轴-
≤1,取一组满足此条件的a,b,c的值即可.
| b |
| 2a |
解答:解:设该函数解析式为:y=ax2+bx+c(a≠0).
由函数图象过点(-2,1),得1=4a-2b+c;由函数在[1,+∞)上减少,得a<0,且对称轴x=-
≤1,即b≤-2a
令a=-1,b=2,则c=9,满足上述条件.
故解析式:y=-x2+2x+9满足要求.
故答案为:y=-x2+2x+9.
由函数图象过点(-2,1),得1=4a-2b+c;由函数在[1,+∞)上减少,得a<0,且对称轴x=-
| b |
| 2a |
令a=-1,b=2,则c=9,满足上述条件.
故解析式:y=-x2+2x+9满足要求.
故答案为:y=-x2+2x+9.
点评:本题考查二次函数的图象及性质,属基础题,深刻理解二次函数的图象及有关性质是解决该类问题的基础.

练习册系列答案
相关题目
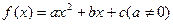 的图象过点
的图象过点 ,且与
,且与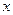 轴有唯一的交点
轴有唯一的交点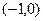 。
。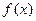 的表达式;
的表达式;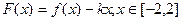 ,记此函数的最小值为
,记此函数的最小值为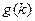 ,求
,求 的图象过点(1,13),图像关于直线
的图象过点(1,13),图像关于直线 对称。
对称。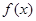 的解析式。
的解析式。 ,
, ,
, 的零点有三个,求实数
的零点有三个,求实数 的取值范围;
的取值范围; 在[
在[ ,2]上的最小值。
,2]上的最小值。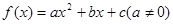 的图象过点
的图象过点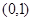 ,且与
,且与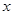 轴有唯一的交点
轴有唯一的交点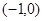 。
。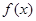 的表达式;
的表达式;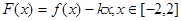 ,记此函数的最小值为
,记此函数的最小值为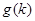 ,求
,求