题目内容
(本小题满分13分)如图,已知圆E: ,点
,点 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.

(Ⅰ)求动点Q的轨迹 的方程;
的方程;
(Ⅱ)设直线 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹 相交于
相交于 两点, 直线
两点, 直线 的斜率分别为
的斜率分别为 (其中
(其中 ).△
).△ 的面积为
的面积为 , 以
, 以 为直径的圆的面积分别为
为直径的圆的面积分别为 .若
.若 恰好构成等比数列, 求
恰好构成等比数列, 求 的取值范围.
的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)  .
.
【解析】
试题分析:(Ⅰ)由垂直平分线性质可知, ,所以有
,所以有 ,由椭圆定义可得点
,由椭圆定义可得点 的轨迹为椭圆,可求其轨迹方程;
的轨迹为椭圆,可求其轨迹方程;
(Ⅱ) 设直线 的方程为
的方程为 ,与椭圆方程联立,由
,与椭圆方程联立,由 及韦达定理可求得
及韦达定理可求得 ,再利用
,再利用 可求出
可求出 的取值范围,求出
的取值范围,求出 ,即可求
,即可求 的取值范围。
的取值范围。
试题解析:(Ⅰ)连结QF,根据题意,|QP|=|QF|,则|QE|+|QF|=|QE|+|QP|=4 ,
,
故动点Q的轨迹 是以E,F为焦点,长轴长为4的椭圆. 2分
是以E,F为焦点,长轴长为4的椭圆. 2分
设其方程为 ,可知
,可知 ,
, ,则
,则 , 3分
, 3分
所以点Q的轨迹 的方程为
的方程为 . 4分
. 4分

(Ⅱ)设直线 的方程为
的方程为 ,
, ,
,
由 可得
可得 ,
,
由韦达定理有:
 且
且 6分
6分
∵ 构成等比数列,
构成等比数列,
 =
= ,即:
,即:
由韦达定理代入化简得: .∵
.∵  ,
,
 . 8分
. 8分
此时 ,即
,即 .又由
.又由 三点不共线得
三点不共线得
从而 .
.
故


 10分
10分
∵
则 



 为定值. 12分
为定值. 12分




 当且仅当
当且仅当 时等号成立.
时等号成立.
综上: 的取值范围是
的取值范围是 . 13分
. 13分
考点:椭圆定义及性质,直线与圆锥曲线关系,基本不等式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案已知:对于给定的 及映射
及映射 ,若集合
,若集合 ,且
,且 中所有元素在B中对应的元素之和大于或等于
中所有元素在B中对应的元素之和大于或等于 ,则称
,则称 为集合
为集合 的好子集.
的好子集.
①对于 ,映射
,映射 ,那么集合
,那么集合 的所有好子集的个数为 ;
的所有好子集的个数为 ;
②对于给定的 ,
, ,映射
,映射 的对应关系如下表:
的对应关系如下表:
| 1 | 2 | 3 | 4 | 5 | 6 |
|
f(x) | 1 | 1 | 1 | 1 | 1 | y | z |
若当且仅当 中含有
中含有 和至少
和至少 中3个整数或者
中3个整数或者 中至少含有
中至少含有 中5个整数时,
中5个整数时, 为集合
为集合 的好子集,则所有满足条件的数组
的好子集,则所有满足条件的数组 为 .
为 .
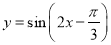 的图象向右平移
的图象向右平移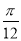 个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为
个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为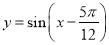
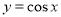
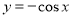
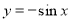
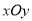 上的区域
上的区域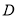 由不等式组
由不等式组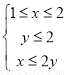 给定.若
给定.若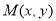 为
为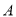 的坐标为
的坐标为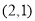 ,则
,则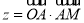 的最大值为( )
的最大值为( ) 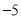 B.
B.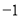 C.
C.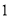 D.
D.
 ,若
,若 ,则
,则 .
. 的图象,只需将函数
的图象,只需将函数 的图象
的图象  个单位长度 B.向左平移
个单位长度 B.向左平移
 个单位长度 D.向左平移
个单位长度 D.向左平移

 , 且
, 且 与
与 在直线l的方向向量上的投影的长度相等,则直线l的斜率为
在直线l的方向向量上的投影的长度相等,则直线l的斜率为 B.
B. C.
C. D.
D.
 ,
, ,则
,则 的值为
的值为 (B)
(B) (C)
(C) (D)
(D)
 及点
及点 .
. 为圆
为圆 上任一点,求
上任一点,求 的最大值和最小值;
的最大值和最小值; ,直线
,直线 与圆C交于点A、B, 当
与圆C交于点A、B, 当 为何值时
为何值时 取到最小值。
取到最小值。