题目内容
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且函数f(x)的图象过点 .
.
(1)求ω和φ的值;
(2)设 ,求函数g(x)的单调递增区间.
,求函数g(x)的单调递增区间.
解:(1)由题意,可知 ,…(2分)
,…(2分)
又∵函数f(x)的图象过点 ,
,
∴ 得,
得, ,得sinφ=1
,得sinφ=1
∵0<φ<π,∴φ= ,…(4分)
,…(4分)
(2)由(1)知: …(6分)
…(6分)
因为 =
=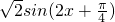 …(9分)
…(9分)
令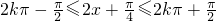 ,得
,得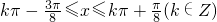 .…(11分)
.…(11分)
∴函数g(x)的单调增区间为 .…(12分)
.…(12分)
分析:(1)根据函数y=Asin(ωx+φ)的周期公式,可得ω=2,再根据f(x)当x= 时函数值等于-1,建立关于φ的等式,结合0<φ<π,即可得到φ的值;
时函数值等于-1,建立关于φ的等式,结合0<φ<π,即可得到φ的值;
(2)根据(1)的结果,代入可得g(x)=cos2x+sin2x,用辅助角公式合并得g(x)=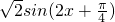 ,最后根据正弦函数单调区间的结论,解不等式即可得到函数g(x)的单调递增区间.
,最后根据正弦函数单调区间的结论,解不等式即可得到函数g(x)的单调递增区间.
点评:本题已知函数y=Asin(ωx+φ)的周期和一个对应值,求函数的表达式,着重考查了三角函数y=Asin(ωx+φ)的图象与性质和正弦函数的单调性等知识,属于基础题.
 ,…(2分)
,…(2分)又∵函数f(x)的图象过点
 ,
,∴
 得,
得, ,得sinφ=1
,得sinφ=1∵0<φ<π,∴φ=
 ,…(4分)
,…(4分)(2)由(1)知:
 …(6分)
…(6分)因为
 =
=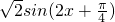 …(9分)
…(9分)令
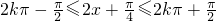 ,得
,得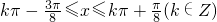 .…(11分)
.…(11分)∴函数g(x)的单调增区间为
 .…(12分)
.…(12分)分析:(1)根据函数y=Asin(ωx+φ)的周期公式,可得ω=2,再根据f(x)当x=
 时函数值等于-1,建立关于φ的等式,结合0<φ<π,即可得到φ的值;
时函数值等于-1,建立关于φ的等式,结合0<φ<π,即可得到φ的值;(2)根据(1)的结果,代入可得g(x)=cos2x+sin2x,用辅助角公式合并得g(x)=
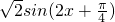 ,最后根据正弦函数单调区间的结论,解不等式即可得到函数g(x)的单调递增区间.
,最后根据正弦函数单调区间的结论,解不等式即可得到函数g(x)的单调递增区间.点评:本题已知函数y=Asin(ωx+φ)的周期和一个对应值,求函数的表达式,着重考查了三角函数y=Asin(ωx+φ)的图象与性质和正弦函数的单调性等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
