Question

已知点F（1，0），直线l：x=-1，点E是l上的动点，过点E垂直于y轴的直线与线段EF的垂直平分线交于点W.

（1）求点W（x，y）的轨迹C的方程.

（2）过点A（2，0）的直线l′与轨迹C交于P、Q两点，且，求点R的轨迹方程.

Answer 1

解：(1)连结WF,?

∵W位于线段EF的垂直平分线上,?

∴|FW|=|WE|,?

∴点W的轨迹是以F为焦点,以直线l为准线的抛物线.?

∵p=2,∴点W(x,y)的轨迹C的方程为y²=4x.?

(2)设P(x₁,y₁),Q(x₂,y₂),R(x,y),?

∵,?

∴(x₁-1,y₁)+(x₂-1,y₂)=(x-1,y),?

∴x₁+x₂-2=x-1,y₁+y₂=y,?

又y₁²=4x₁,y₂²=4x₂两式相减得(y₁+y₂)(y₁-y₂)=4(x₁-x₂),当x₁≠x₂时,.  ①?

又由平行四边形的性质得FR的中点M(也是QP的中点)在直线QP上.?

∴k_QP=k_AM ,即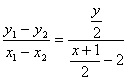.                                     ②?

把①代入②得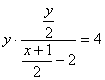，整理得y²=4x-12.当x₁=x₂时,点R的坐标为(3,0),也适合方程y²=4x-12.综上所述,点R的轨迹方程y²=4x-12.