题目内容
已知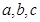 是正数,
是正数,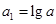 ,
,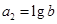 ,
,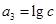 .
.
(Ⅰ)若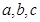 成等差数列,比较
成等差数列,比较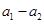 与
与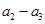 的大小;
的大小;
(Ⅱ)若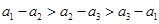 ,则
,则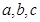 三个数中,哪个数最大,请说明理由;
三个数中,哪个数最大,请说明理由;
(Ⅲ)若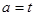 ,
,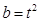 ,
,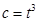 (
(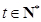 ),且
),且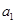 ,
,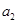 ,
,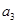 的整数部分分别是
的整数部分分别是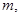
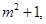
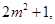 求所有
求所有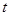 的值.
的值.
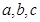 是正数,
是正数,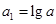 ,
,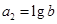 ,
,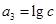 .
.(Ⅰ)若
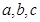 成等差数列,比较
成等差数列,比较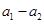 与
与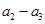 的大小;
的大小;(Ⅱ)若
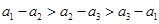 ,则
,则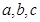 三个数中,哪个数最大,请说明理由;
三个数中,哪个数最大,请说明理由;(Ⅲ)若
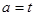 ,
,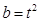 ,
,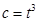 (
(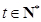 ),且
),且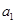 ,
,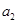 ,
,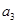 的整数部分分别是
的整数部分分别是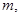
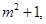
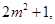 求所有
求所有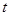 的值.
的值.(Ⅰ)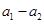
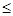
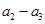 ;(Ⅱ)
;(Ⅱ)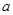 最大;(Ⅲ)
最大;(Ⅲ)
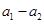
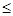
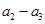 ;(Ⅱ)
;(Ⅱ)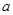 最大;(Ⅲ)
最大;(Ⅲ)
试题分析:(Ⅰ)用作差法比较大小,用对数的运算法则化简后与0作比较。此时只需对数的真数与1作比较即可,根据单调性比得出对数和0的大小,从而得出
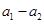 与
与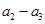 的大小。(Ⅱ)运用对数的运算法则将不等式化简,再根据对数的单调性得真数的不等式,即关于a,b,c的不等式通过整理即可比较出三者中谁最大。(Ⅲ)由已知可得
的大小。(Ⅱ)运用对数的运算法则将不等式化简,再根据对数的单调性得真数的不等式,即关于a,b,c的不等式通过整理即可比较出三者中谁最大。(Ⅲ)由已知可得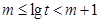 ,根据对数的运算法则可得
,根据对数的运算法则可得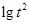 的范围,得到其整数部分,根据已知其整数部分可列式求得
的范围,得到其整数部分,根据已知其整数部分可列式求得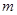 的可能取值。然后分情况讨论,解对数不等式可求得
的可能取值。然后分情况讨论,解对数不等式可求得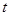 的值。
的值。试题解析:解:(Ⅰ)由已知得
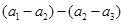 =
=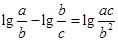 .
.因为
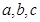 成等差数列,所以
成等差数列,所以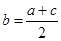 ,
,则
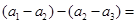
 ,
,因为
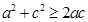 ,所以
,所以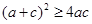 ,即
,即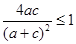 ,
,则
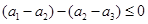 ,即
,即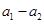
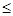
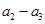 ,当且仅当
,当且仅当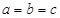 时等号成立.
时等号成立.4分
(Ⅱ)解法1:令
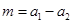 ,
,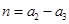 ,
,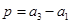 ,
,依题意,
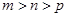 且
且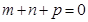 ,所以
,所以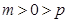 .
.故
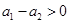 ,即
,即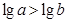 ;且
;且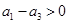 ,即
,即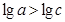 .
.所以
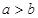 且
且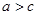 .
.故
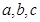 三个数中,
三个数中,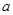 最大.
最大.解法2:依题意
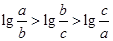 ,即
,即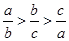 .
.因为
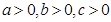 ,所以
,所以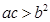 ,
,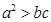 ,
,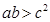 .
.于是,
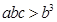 ,
,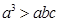 ,
,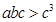 ,
,所以
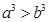 ,
,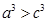 .
.因为
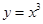 在
在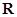 上为增函数,所以
上为增函数,所以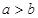 且
且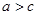 .
.故
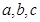 三个数中,
三个数中,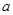 最大. 8分
最大. 8分(Ⅲ)依题意,
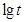 ,
,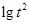 ,
,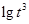 的整数部分分别是
的整数部分分别是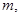
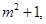
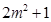 ,则
,则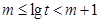 ,
,所以
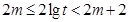 .
.又
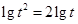 ,则
,则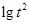 的整数部分是
的整数部分是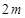 或
或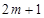 .
.当
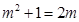 时,
时,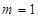 ;
;当
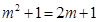 时,
时,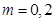 .
.当
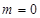 时,
时,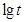 ,
,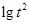 ,
,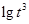 的整数部分分别是
的整数部分分别是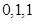 ,
,所以
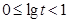 ,
,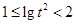 ,
,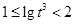 .所以
.所以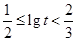 ,解得
,解得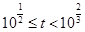 .
.又因为
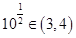 ,
,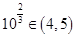 ,所以此时
,所以此时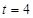 .
.(2)当
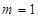 时,同理可得
时,同理可得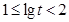 ,
,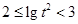 ,
,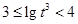 .
.所以
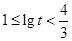 ,解得
,解得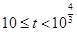 .又
.又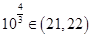 ,此时
,此时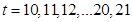 .
.(3)当
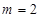 时,同理可得
时,同理可得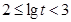 ,
,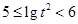 ,
,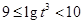 ,
,同时满足条件的
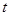 不存在.
不存在.综上所述
 . 13分
. 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,不等式
,不等式 成立,则实数a的取值范围是_____________.
成立,则实数a的取值范围是_____________. (2m-4)+log
(2m-4)+log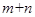 的最小值为 .
的最小值为 . ,则( )
,则( )



 ,若
,若 ,则
,则 _________.
_________. 的解集为_____________.
的解集为_____________.