题目内容
如图,已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°,且AB∥CD,AB=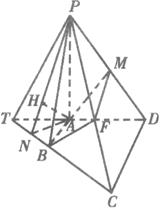
(1)点F在线段PC上运动,且设![]() =λ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
=λ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
(2)若二面角F-CD-B为45°,求二面角B-PC-D的大小;
(3)在(2)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
解:(1)当λ=1时,即F为PC的中点时,BF∥面PAD,取PD的中点为M,连FM,AM.∵FM∥CD∥AB,FM=![]() CD=AB,∴四边形ABFM为平行四边形,∴BF∥AM,又AM
CD=AB,∴四边形ABFM为平行四边形,∴BF∥AM,又AM![]() 面PAD,BF
面PAD,BF![]() 面PAD,∴BF∥面PAD.
面PAD,∴BF∥面PAD.

(2)易证∠PDA为二面角F-CD-B的平面角,∴∠PDA=45 ,又M为PD的中点,∴AM⊥PD,又CD⊥面PAD,∴AM⊥CD,∴AM⊥面PCD.∵AM∥BF,∴BF⊥面PCD,BF![]() 面PBC,∴平面PBC⊥面PCD,即二面角B-PC-D为90°.
面PBC,∴平面PBC⊥面PCD,即二面角B-PC-D为90°.
(3)延长CB交DA于T点,作AN⊥TB,连PN,则TBPAN,作AH⊥PN于H点,则AH⊥面PBC,即AH为点平面PBC的距离.
PA=AD=AT=2,AB=![]() ,AN=
,AN=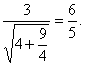 ∴AH=
∴AH=![]()
或等体积法VA-PBC=VP-ABC或建系均可.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,