题目内容
已知数列{an}满足a1= ,an=
,an=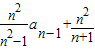 (n≥2,n∈N*),数列{bn}的前n项和Sn,满足:
(n≥2,n∈N*),数列{bn}的前n项和Sn,满足: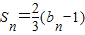 .
.(I)求数列{an}、{bn}的通项公式an,bn;
(II)设
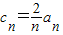 ,①求数列{bncn}前n项的和Tn,②求数列
,①求数列{bncn}前n项的和Tn,②求数列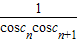 前n项的和An.
前n项的和An.
【答案】分析:(I)把式子变形,构造数列{dn}由累加法可得an,由数列的通项和前n想和的关系可得bn;
(II)①由数列{bncn}的特点,用错位相减法可求和,②式子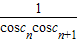 可化为
可化为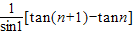 ,下面用裂项相消法可得答案.
,下面用裂项相消法可得答案.
解答:解:(I)因为an=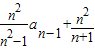 (n≥2,n∈N*),
(n≥2,n∈N*),
所以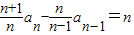 ,设
,设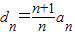 ,
,
则dn-dn-1=n(n≥2,n∈N*),d1=1,
由累加法可得: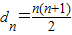 ,故
,故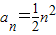
∵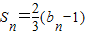 ①,∴
①,∴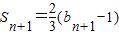 ②
②
②-①得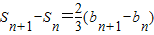 =bn+1,∴bn+1=-2bn
=bn+1,∴bn+1=-2bn
把n=1代入①式可得b1=-2,
∴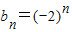
(II)由(I)可知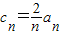 =
=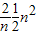 =n
=n
①bncn=n•(-2)n
∴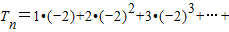 n•(-2)n
n•(-2)n
-2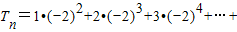 n•(-2)n+1
n•(-2)n+1
两式相减得: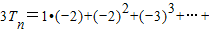 (-2)n-n•(-2)n+1
(-2)n-n•(-2)n+1
=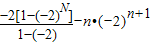 =
=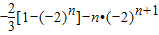
故所求数列的前n项和为: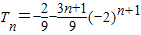
②∵sin1=sin[(n+1)-n]=sin(n+1)cosn-cos(n+1)sinn
∴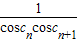 =
=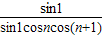 =
=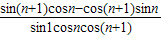
=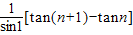
故所求数列的前n项和为:
An=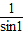 [(tan2-tan1)+(tan3-tan2)+…+(tan(n+1)-tann)]
[(tan2-tan1)+(tan3-tan2)+…+(tan(n+1)-tann)]
=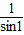 [tan(n+1)-tann]
[tan(n+1)-tann]
点评:本题为数列的综合应用,涉及累加法,错位相减法,裂项相消法,属中档题.
(II)①由数列{bncn}的特点,用错位相减法可求和,②式子
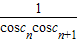 可化为
可化为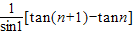 ,下面用裂项相消法可得答案.
,下面用裂项相消法可得答案.解答:解:(I)因为an=
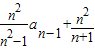 (n≥2,n∈N*),
(n≥2,n∈N*),所以
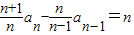 ,设
,设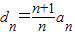 ,
,则dn-dn-1=n(n≥2,n∈N*),d1=1,
由累加法可得:
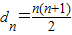 ,故
,故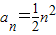
∵
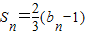 ①,∴
①,∴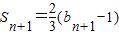 ②
②②-①得
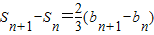 =bn+1,∴bn+1=-2bn
=bn+1,∴bn+1=-2bn把n=1代入①式可得b1=-2,
∴
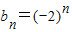
(II)由(I)可知
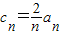 =
=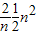 =n
=n①bncn=n•(-2)n
∴
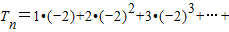 n•(-2)n
n•(-2)n-2
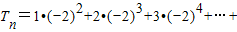 n•(-2)n+1
n•(-2)n+1两式相减得:
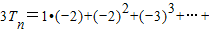 (-2)n-n•(-2)n+1
(-2)n-n•(-2)n+1=
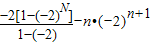 =
=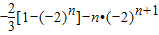
故所求数列的前n项和为:
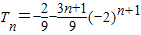
②∵sin1=sin[(n+1)-n]=sin(n+1)cosn-cos(n+1)sinn
∴
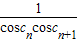 =
=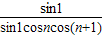 =
=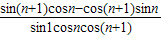
=
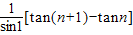
故所求数列的前n项和为:
An=
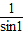 [(tan2-tan1)+(tan3-tan2)+…+(tan(n+1)-tann)]
[(tan2-tan1)+(tan3-tan2)+…+(tan(n+1)-tann)]=
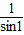 [tan(n+1)-tann]
[tan(n+1)-tann]点评:本题为数列的综合应用,涉及累加法,错位相减法,裂项相消法,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目