题目内容
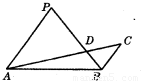
如图，若PA=PB，∠APB=2∠ACB，AC与PB交于点D，且PB=4，PD=3，则AD•DC=7
7
．分析：以P为圆心，以PA=PB为半径作圆，延长BD交圆于M，如图，证明C在圆上，利用AD•DC=BD•DM来求出它的值．
解答：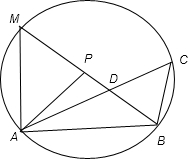
解：以P为圆心，以PA=PB为半径作圆，延长BD交圆于M，如图：PA=PB=4，∠APB=2∠ACB，AC与PB交于点D，PD=3，
设∠ACB=θ，则∠APB=2θ，又∠ACB=θ，∴C在圆上．
∴AD•DC=BD•DM=BD•（PM+PD）=1•（4+3）=7，
故答案为 7．
解：以P为圆心，以PA=PB为半径作圆，延长BD交圆于M，如图：PA=PB=4，∠APB=2∠ACB，AC与PB交于点D，PD=3，设∠ACB=θ，则∠APB=2θ，又∠ACB=θ，∴C在圆上．
∴AD•DC=BD•DM=BD•（PM+PD）=1•（4+3）=7，
故答案为 7．
点评：本题主要考查四点共圆的性质与相似三角形的性质，属于中等题．温馨提示：四点共圆时四边形对角互补，圆与三角形综合问题是高考中平面几何选讲的重要内容，也是考查的热点．
练习册系列答案
相关题目
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
选做题（请考生在三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）．
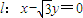与曲线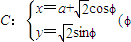
为参数，a＞0）有两个公共点A、B，且|AB|=2，则实数a的值为 ．