Question

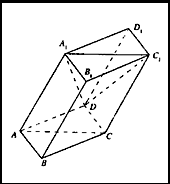（本小题满分12分） 如图，棱柱的所有棱长都等于，，平面⊥平面，。

（1）证明：；（2）求二面角的平面角的余弦值；（3）在直线上是否存在点，使平面？若存在，求出点的位置；若不存在，说明理由。

Answer 1

(Ⅰ)  见解析  (Ⅱ)  （Ⅲ）点P在C₁C的延长线上且使C₁C=CP

解析:

：连接BD交AC于O,则BD⊥AC,连接A₁O. 在△AA₁O中,AA₁=2,AO=1,∠A₁AO=60°.

    ∴A₁O²=AA₁²+AO²－2AA₁·Aocos60°=3   ∴AO²+A₁O²=A₁²    ∴A₁O⊥AO，

    由于平面AA₁C₁C⊥平面ABCD，  所以A₁O⊥底面ABCD

    ∴以OB、OC、OA₁所在直线为x轴、y轴、z轴建立空间直角坐标系，

    则A（0，－1，0），B（，0，0），C（0，1，0），D（－，0，0），A₁（0，0，）  1）由于,,

    则

∴BD⊥AA₁                ……………………4分

2）由于OB⊥平面AA₁C₁C,  ∴平面AA₁C₁C的法向量,设⊥平面AA₁D

    则得到   ………6分

   

    所以二面角D—A₁A—C的平面角的余弦值是    ………8分

3）假设在直线CC₁上存在点P，使BP//平面DA₁C₁

    设则得  ……9分

    设则设

    得到    ……………………10分

    又因为平面DA₁C₁   则·

    即点P在C₁C的延长线上且使C₁C=CP  ………………12分