题目内容
设sinα>0,cosα<0,且sin
>cos
,则
的取值范围是( )
| α |
| 3 |
| α |
| 3 |
| α |
| 3 |
A.(2kπ+
| ||||||||
B.(
| ||||||||
C.(2kπ+
| ||||||||
D.(2kπ+
|
∵sin
>cos
,
∴
+2kπ<
<
+2kπ,k∈Z,
∴
+6kπ<α<
+6kπ,k∈Z,①
又sinα>0,cosα<0,
∴α是第二象限角,②
由①②可得:
+6kπ<α<π+6kπ,或
+6kπ<α<3π+6kπ,k∈Z,
∴2kπ+
<
<2kπ+
或2kπ+
<
<2kπ+π,k∈Z
故选D.
| α |
| 3 |
| α |
| 3 |
∴
| π |
| 4 |
| α |
| 3 |
| 5π |
| 4 |
∴
| 3π |
| 4 |
| 15π |
| 4 |
又sinα>0,cosα<0,
∴α是第二象限角,②
由①②可得:
| 3π |
| 4 |
| 5π |
| 2 |
∴2kπ+
| π |
| 4 |
| α |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| α |
| 3 |
故选D.

练习册系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤. 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E: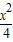
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.
 把圆C:x2+y2=1变换为椭圆E:
把圆C:x2+y2=1变换为椭圆E:
 =1.
=1. 求实数a的值.
求实数a的值. ≥4.
≥4.