题目内容
在△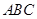 中,三个内角
中,三个内角 ,
, ,
, 的对边分别为
的对边分别为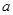 ,
,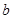 ,
,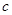 ,
,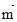 =(b,
=(b,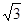 a),
a),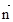 =(cosB,sinA),且
=(cosB,sinA),且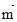 ||
||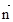 (Ⅰ)求角
(Ⅰ)求角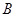 ;(Ⅱ)若
;(Ⅱ)若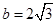 ,c=2a, 求△
,c=2a, 求△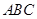 的面积.
的面积.
【答案】
(Ⅰ) ;(Ⅱ)面积为
;(Ⅱ)面积为 .
.
【解析】
试题分析:(Ⅰ)由向量平行的条件及题设可得 ,再由正弦定理可得
,再由正弦定理可得 , 约掉
, 约掉 即可求得角B;(Ⅱ)由于已知了
即可求得角B;(Ⅱ)由于已知了 ,
,  ,c=2a,显然用余弦定理,可得
,c=2a,显然用余弦定理,可得  ,又因为c=2a,所以a=2,c=4,由此可得△
,又因为c=2a,所以a=2,c=4,由此可得△ 的面积.
的面积.
试题解析:(Ⅰ)因为 =(b,
=(b, a),
a), =(cosB,sinA)且
=(cosB,sinA)且 ||
||

 ,2分
,2分
由正弦定理可得 ,
4分
,
4分
因为在△ 中,
中, ,
,
所以 .5分
.5分
又 ,
,
所以 .6分
.6分
(Ⅱ)由余弦定理  ,
,
因为 ,
, ,
,
所以 .8分
.8分
又因为c=2a,所以a=2,c=4,10分
△ 的面积为S=
的面积为S= 12分
12分
考点:1、等差数列等比数列的通项公式;2、错位相消法求和.

练习册系列答案
相关题目
在△ABC中,三个内角A,B,C依次成等差数列,若sin2B=sinAsinC,则△ABC形状是( )
| A、锐角三角形 | B、等边三角形 | C、直角三角形 | D、等腰直角三角形 |