题目内容
已知x∈R,用[x]表示不超过x的最大整数,记{x}=x-[x],若a∈(0,1),则{a}与{a+
}的大小关系是( )
| 1 |
| 2 |
| A、不确定(与a的值有关) | ||
B、{a}<{a+
| ||
C、{a}={a+
| ||
D、{a}>{a+
|
分析:根据{x}=x-[x],以及a∈(0,1),令a=
和
,分别求出{a}与{a+
}的值,比较大小即可得到结论.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:若a=
,则{a}=a-[a]=
,
此时{a+
}=
>{a},
若a=
,则{a}=a-[a]=
,
此时{a+
}=0<{a},
故{a}与{a+
}的大小关系不确定,
故选A.
| 1 |
| 3 |
| 1 |
| 3 |
此时{a+
| 1 |
| 2 |
| 5 |
| 6 |
若a=
| 1 |
| 2 |
| 1 |
| 2 |
此时{a+
| 1 |
| 2 |
故{a}与{a+
| 1 |
| 2 |
故选A.
点评:此题考查不等式比较大小,对于选择题而言,解决此类问题的方法一般采取特殊值法,属基础题.

练习册系列答案
相关题目
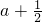 的大小关系是
的大小关系是 的大小关系是( )
的大小关系是( )

