Question

已知A、B是抛物线x²=4y上的两点，线段AB的中点为M（2，2），则|AB|等于________．

Answer 1

分析：设A（x₁，y₁），B（x₂，y₂）
（法一）：由x₁²=4y₁，x₂²=4y₂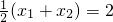，两式相减，结合中点坐标公式可求直线AB的斜率，进而可求直线AB的方程，联立直线与抛物线的方程，可求A，B的坐标，从而可求AB
（法二）由题意可得直线AB的斜率存在，故可设直线AB的方程为y-2=k（x-2）
联立方程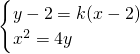整理可得x²-4kx+8（k-1）=0，由方程的跟与系数关系及中点坐标公式，可求直线AB的斜率，及直线AB的方程，进而可求AB
解答：设A（x₁，y₁），B（x₂，y₂）
（法一）：则x₁²=4y₁，x₂²=4y₂，
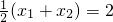
两式相减可得，（x₁-x₂）（x₁+x₂）=4（y₁-y₂）
==1
直线AB的方程为y-2=x-2即x-y=0
联立方程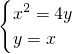可得x²=4x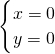

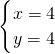
AB=
（法二）由题意可得直线AB的斜率存在，故可设直线AB的方程为y-2=k（x-2）
联立方程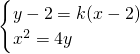整理可得x²-4kx+8（k-1）=0
x₁+x₂=4k
由中点坐标公式可得
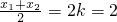
k=1
以下同法一的求解
故答案为：
点评：本题主要考查了直线与曲线相交求解弦长问题，解决此类问题最一般的方法是联立直线与曲线方程，结合方程的根与系数关系及弦长公式可求，要注意方法一中“设而不求”方法的应用．