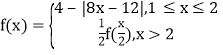题目内容
【题目】已知函数![]() ,若函数
,若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,则实数
,则实数![]() 的取值范围是________.
的取值范围是________.
【答案】![]()
【解析】
由题意可得![]() ,
,![]() ,作比得
,作比得![]() =
=![]() =
=![]() ,令
,令![]() =t,结合条件将
=t,结合条件将![]() 写成关于t的函数,求导分析得到
写成关于t的函数,求导分析得到![]() 的范围,再结合
的范围,再结合![]() 得到a的范围,与函数
得到a的范围,与函数![]() 有两个极值点时a的范围取交集即可.
有两个极值点时a的范围取交集即可.
∵函数![]() 有两个极值点
有两个极值点![]() ,∴
,∴![]() 有两个零点
有两个零点![]() ,
,
即![]() ,
,![]() 两式作比得到:
两式作比得到:![]() =
=![]() =
=![]() ,
,
令![]() =t
=t![]() ,则有
,则有![]() =
=![]() , ②
, ②
∴![]() 代入
代入![]() 式得:
式得:![]() ,
,
又由②得![]() =
=![]() ,∴t
,∴t![]() ,
,
令g(t)=![]() t
t![]() ,则
,则![]() =
=![]() ,
,
令h(t)=![]() ,则
,则![]() =
=![]() ,
,
∴h(t)单调递减,∴h(t)![]() =1-2
=1-2![]() ,
,
∴g(t)单调递减,∴g(t)![]() =
=![]() ,即
,即![]() ,
,
而![]() ,令u(x)=
,令u(x)=![]() ,则
,则![]() >0, ∴u(x)在x
>0, ∴u(x)在x![]() 上单调递增,
上单调递增,
∴u(x)![]() ,即a
,即a![]() ,
,
又![]() 有两个零点
有两个零点![]() ,u(x)在R上与y=a有两个交点,
,u(x)在R上与y=a有两个交点,
而![]() ,在(-
,在(-![]() ,1)
,1)![]() , u(x) 单调递增,在(1,+
, u(x) 单调递增,在(1,+![]() , u(x)单调递减,u(x)的最大值为u(1)=
, u(x)单调递减,u(x)的最大值为u(1)=![]() ,大致图像为:
,大致图像为:

∴![]() ,又
,又![]() ,
,![]() ,
,
综上,![]() ,
,
故答案为![]() .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目