题目内容
19.已知函数f(x)=ax7+bx5+x2(ab≠0),f(2)=-1,求f(-2)分析 由已知条件利用函数性质求出128a+32b=-5,由此能求出f(-2).
解答 解:∵f(x)=ax7+bx5+x2(ab≠0),f(2)=-1,
∴f(2)=128a+32b+4=-1,
∴128a+32b=-5,
∴f(-2)=-128a-32b+4=5+4=9.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
9.已知f(x)是定义在R上的偶函数且在[0,+∞)上递增,p:f($\frac{x}{x+1}$)<f(-$\frac{1}{2}$),q:|x-a|<1,若p是q的充分不必要条件,则实数a的取值范围为( )
| A. | (0,$\frac{4}{3}$) | B. | (-∞,0)∪($\frac{4}{3}$,+∞) | C. | (-∞,0]∪[$\frac{4}{3}$,+∞) | D. | [0,$\frac{2}{3}$] |
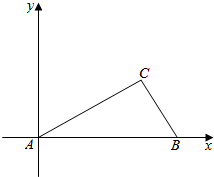 如图,一边在x轴,一个顶点在原点△ABC的所有高都小于1,请问是否存在这样的B、C的位置,使得△ABC的面积大于2015?
如图,一边在x轴,一个顶点在原点△ABC的所有高都小于1,请问是否存在这样的B、C的位置,使得△ABC的面积大于2015?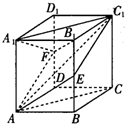 如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.