题目内容
已知f(x)是定义在[-2,2]上的函数,且对任意实数x1,x2(x1≠x2),恒有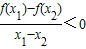 ,且f(x)的最大值为1,则满足f(
,且f(x)的最大值为1,则满足f(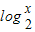 )<1的解集为 .
)<1的解集为 .
【答案】分析:由题意,得f(x)是定义在[-2,2]上的减函数,可得f(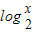 )<1即f(
)<1即f(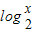 )<f(-2),结合函数的单调性转化为-2<
)<f(-2),结合函数的单调性转化为-2<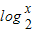 ≤2,解之即可得到所求的解集.
≤2,解之即可得到所求的解集.
解答:解:∵对任意实数x1,x2(x1≠x2),恒有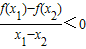 ,
,
∴f(x)是定义在[-2,2]上的减函数,得函数的最大值为f(-2)=1
∴f(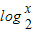 )<1即f(
)<1即f(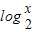 )<f(-2)
)<f(-2)
结合函数的单调性,得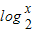 >-2,即
>-2,即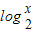 >
>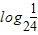 ,解之得x
,解之得x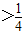
又∵f(x)定义在[-2,2]上,
∴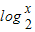 ∈[-2,2],解之得
∈[-2,2],解之得 ≤x≤4
≤x≤4
取交集,得 <x≤4,原不等式的解集为
<x≤4,原不等式的解集为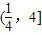
故答案为: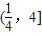
点评:本题给出抽象函数,在已知单调性的情况下求解不等式,着重考查了对数的运算法则和函数的单调性等知识,属于中档题.
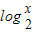 )<1即f(
)<1即f(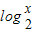 )<f(-2),结合函数的单调性转化为-2<
)<f(-2),结合函数的单调性转化为-2<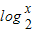 ≤2,解之即可得到所求的解集.
≤2,解之即可得到所求的解集.解答:解:∵对任意实数x1,x2(x1≠x2),恒有
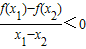 ,
,∴f(x)是定义在[-2,2]上的减函数,得函数的最大值为f(-2)=1
∴f(
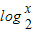 )<1即f(
)<1即f(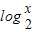 )<f(-2)
)<f(-2)结合函数的单调性,得
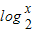 >-2,即
>-2,即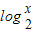 >
>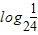 ,解之得x
,解之得x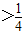
又∵f(x)定义在[-2,2]上,
∴
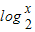 ∈[-2,2],解之得
∈[-2,2],解之得 ≤x≤4
≤x≤4取交集,得
 <x≤4,原不等式的解集为
<x≤4,原不等式的解集为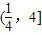
故答案为:
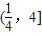
点评:本题给出抽象函数,在已知单调性的情况下求解不等式,着重考查了对数的运算法则和函数的单调性等知识,属于中档题.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目