题目内容
定义在[-1,1]的偶函数f(x),当x∈[0,1]时为减函数,则不等式:f(
-x)<f(x)的解集为 .
| 1 | 2 |
分析:根据函数f(x)为偶函数且在[0,1]上为减函数,可得f(x)在区间[-1,0]上为增函数.由此作出草图加以理解,建立关于x的不等式组,解之即可得出原不等式的解集.
解答:解:∵偶函数f(x)当x∈[0,1]时为减函数,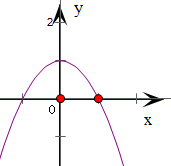
∴当x∈[-1,0]时,f(x)为增函数,
得不等式f(
-x)<f(x),可化为:|x|<|
-x|
解之得x<
又∵偶函数f(x)定义在[-1,1]上,
∴
,解之得-
≤x≤1
综上所述,不等式f(
-x)<f(x)的解集为[-
,
)
故答案为:[-
,
)

∴当x∈[-1,0]时,f(x)为增函数,
得不等式f(
| 1 |
| 2 |
| 1 |
| 2 |
解之得x<
| 1 |
| 4 |
又∵偶函数f(x)定义在[-1,1]上,
∴
|
| 1 |
| 2 |
综上所述,不等式f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:[-
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题给出偶函数满足的条件,求解关于x的不等式,着重考查了函数的奇偶性、单调性和不等式的解法等知识,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
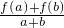 >0成立.
>0成立. )<f(
)<f( );
); >0成立.
>0成立. )<f(
)<f( );
); >0成立.
>0成立. )<f(
)<f( );
);