题目内容
设二次函数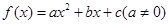 满足条件:①当
满足条件:①当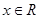 时,
时,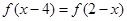 ,且
,且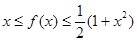 ;②
;② 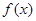 在
在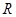 上的最小值为
上的最小值为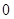 。(1)求
。(1)求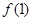 的值及
的值及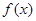 的解析式;(2)若
的解析式;(2)若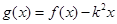 在
在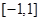 上是单调函数,求
上是单调函数,求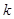 的取值范围;(3)求最大值
的取值范围;(3)求最大值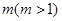 ,使得存在
,使得存在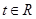 ,只要
,只要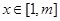 ,就有
,就有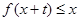 。
。
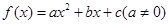 满足条件:①当
满足条件:①当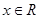 时,
时,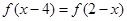 ,且
,且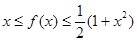 ;②
;② 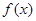 在
在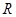 上的最小值为
上的最小值为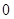 。(1)求
。(1)求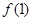 的值及
的值及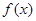 的解析式;(2)若
的解析式;(2)若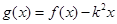 在
在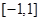 上是单调函数,求
上是单调函数,求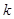 的取值范围;(3)求最大值
的取值范围;(3)求最大值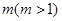 ,使得存在
,使得存在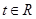 ,只要
,只要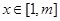 ,就有
,就有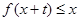 。
。(1) ∵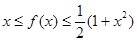 在
在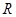 上恒成立,∴
上恒成立,∴
即 ……………(1分)
……………(1分)
∵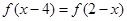 ,∴函数图象关于直线
,∴函数图象关于直线 对称,
对称,
∴ ……………(2分)
……………(2分)
∵ ,∴
,∴
又∵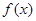 在
在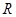 上的最小值为
上的最小值为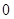 ,∴
,∴ ,即
,即 ,……………(3分)
,……………(3分)
由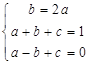 解得
解得 ,∴
,∴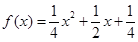 ;……………(4分)
;……………(4分)
(2)∵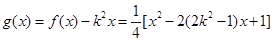 ,
,
∴ 对称轴方程为
对称轴方程为 ,……………(5分)
,……………(5分)
∵ 在
在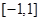 上是单调函数,∴
上是单调函数,∴ 或
或 ,……………(7分)
,……………(7分)
∴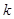 的取值范围是
的取值范围是 或
或 或
或 。……………(8分)
。……………(8分)
(3)∵当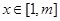 时,
时, 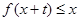 恒成立,∴
恒成立,∴ 且
且 ,
,
由 得
得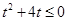 ,解得
,解得 ……………(9分)
……………(9分)
由 得:
得: ,
,
解得 ,……………(10分)
,……………(10分)
∵ ,∴
,∴ ,……………(11分)
,……………(11分)
当 时,对于任意
时,对于任意 ,恒有
,恒有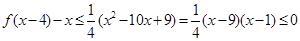 ,
,
∴ 的最大值为
的最大值为 .……………(12分)
.……………(12分)
另解: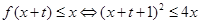 且
且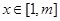

 在
在 上恒成立
上恒成立

∵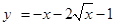 在
在 上递减,∴
上递减,∴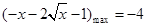 ,
,
∵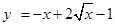 在
在 上递减,∴
上递减,∴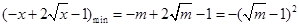
∴ ,∴
,∴ ,
, ,∵
,∵ ,∴
,∴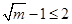 ,
,
∴ ,∴
,∴ 的最大值为
的最大值为
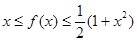 在
在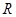 上恒成立,∴
上恒成立,∴
即
 ……………(1分)
……………(1分)∵
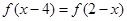 ,∴函数图象关于直线
,∴函数图象关于直线 对称,
对称,∴
 ……………(2分)
……………(2分)∵
 ,∴
,∴
又∵
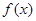 在
在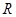 上的最小值为
上的最小值为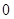 ,∴
,∴ ,即
,即 ,……………(3分)
,……………(3分)由
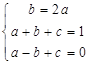 解得
解得 ,∴
,∴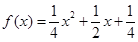 ;……………(4分)
;……………(4分)(2)∵
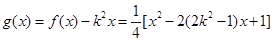 ,
,∴
 对称轴方程为
对称轴方程为 ,……………(5分)
,……………(5分)∵
 在
在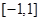 上是单调函数,∴
上是单调函数,∴ 或
或 ,……………(7分)
,……………(7分)∴
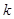 的取值范围是
的取值范围是 或
或 或
或 。……………(8分)
。……………(8分)(3)∵当
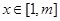 时,
时, 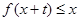 恒成立,∴
恒成立,∴ 且
且 ,
,由
 得
得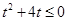 ,解得
,解得 ……………(9分)
……………(9分)由
 得:
得: ,
,解得
 ,……………(10分)
,……………(10分)∵
 ,∴
,∴ ,……………(11分)
,……………(11分)当
 时,对于任意
时,对于任意 ,恒有
,恒有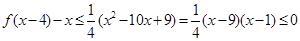 ,
,∴
 的最大值为
的最大值为 .……………(12分)
.……………(12分)另解:
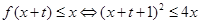 且
且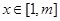

 在
在 上恒成立
上恒成立

∵
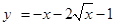 在
在 上递减,∴
上递减,∴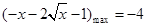 ,
,∵
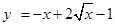 在
在 上递减,∴
上递减,∴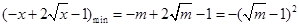
∴
 ,∴
,∴ ,
, ,∵
,∵ ,∴
,∴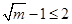 ,
,∴
 ,∴
,∴ 的最大值为
的最大值为
略

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
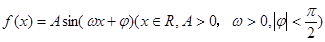 的图象(部分)如图所示,则
的图象(部分)如图所示,则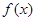 的解析式是
的解析式是



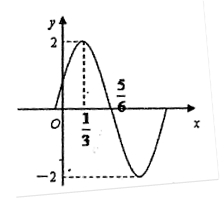
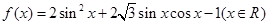 .
.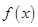 的图像是由函数
的图像是由函数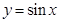 的图像经过怎样的变换得到的;
的图像经过怎样的变换得到的;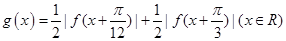 ,试判断函数
,试判断函数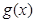 的奇偶性,并用反证法证明函数
的奇偶性,并用反证法证明函数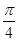 ;
;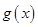 的单调区间和值域.
的单调区间和值域.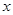 (百万元)请李子恒老师进行创作,经调研知:该唱片的总利润
(百万元)请李子恒老师进行创作,经调研知:该唱片的总利润 (百万元)与
(百万元)与 成正比的关系,当
成正比的关系,当 时
时 .又有
.又有 ,其中
,其中 是常数,且
是常数,且 .
. ,求其表达式,定义域(用
,求其表达式,定义域(用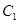 :
: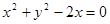 与曲线
与曲线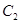 :
: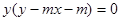 有4个不同的交点,则实数
有4个不同的交点,则实数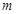 的取值范围为( )
的取值范围为( )



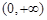 的单调函数
的单调函数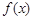 满足:
满足: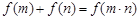 对任意
对任意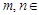
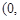
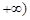 均成立.
均成立.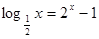 的实数根的个数为( )
的实数根的个数为( )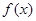 和
和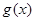 对其定义域上的任意实数x恒有:
对其定义域上的任意实数x恒有: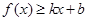 和
和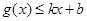 ,则称直线
,则称直线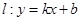 为
为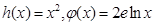 ,则可推知
,则可推知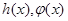 的“隔离直线”方程为 ▲
的“隔离直线”方程为 ▲ 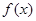 ,
,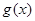 分别由下表给出
分别由下表给出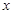
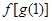 的值为
的值为