题目内容
设y=f(x)是定义在区间[-1,1]上的函数,且满足条件:
(i)f(-1)=f(1)=0;
(ii)对任意的u,v∈[-1,1],都有|f(u)-f(v)|≤|u-v|.
(Ⅰ)证明:对任意的x∈[-1,1],都有x-1≤f(x)≤1-x;
(Ⅱ)判断函数g(x)=![]() 是否满足题设条件;
是否满足题设条件;
(Ⅲ)在区间[-1,1]上是否存在满足题设条件的函数y=f(x),且使得对任意的u,v∈[-1,1],都有|f(u)-f(v)|=|u-v|.
若存在,请举一例;若不存在,请说明理由.
答案:
解析:
解析:
(Ⅰ)证明:由题设条件可得,当x∈[-1,1]时,有 即 (Ⅱ)答:函数g(x)满足题设条件,验证如下:g(-1)=0=g(1). 对任意的 当 当 当u·v<0时,不妨设u∈[-1,0],v∈(0,1], 有|g(u)-g(v)|=|(1+u)-(1-v)|=|u+v|≤|v-u|. 所以,函数g(x)满足题设条件. (Ⅲ)答:这样的函数不存在.理由如下: 假设存在f(x)满足条件,则由f(-1)=f(1)=0 , 得| f(1)-f(-1)|=0 ① 由于对任意的u,v∈[-1,1],都有|f(u)-f(v)|=|u-v|, 所以,|f(1)-f(-1)|=|1-(-1)|=2. ② ①与②矛盾,因此假设不成立, 即这样的函数不存在.
|

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题: ,
, = .
= .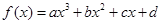 (
(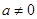 ),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数
),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数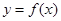 的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数
的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数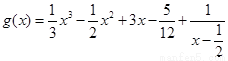 ,则
,则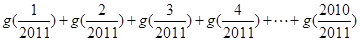 =( )
=( ) (
( ),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数
),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数 的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数
的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数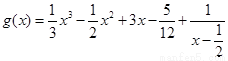 ,则
,则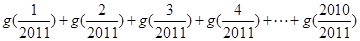 =( )
=( )