题目内容
下列函数中,在其定义域内既是增函数又是奇函数的是
- A.

- B.y=log2(x-1)
- C.

- D.
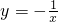
A
分析:逐个验证:选项A,满足f(-x)+f(x)= +
+ =0,故为奇函数,由复合函数的单调性可知为增函数,故符合要求;选项B非奇非偶;选项C不是奇函数;选项D,在(-∞,0)和(0,+∞)上均为增函数,但在整个定义域上没有单调性.
=0,故为奇函数,由复合函数的单调性可知为增函数,故符合要求;选项B非奇非偶;选项C不是奇函数;选项D,在(-∞,0)和(0,+∞)上均为增函数,但在整个定义域上没有单调性.
解答:选项A,定义域为R,且满足f(-x)+f(x)= +
+
=ln(x2+1-x2)=ln1=0,故函数为奇函数,
又函数y= 为增函数,由复合函数的单调性可知,函数为增函数,故符合要求;
为增函数,由复合函数的单调性可知,函数为增函数,故符合要求;
选项B,在定义域(1,+∞)为增函数,但非奇非偶,故不合题意;
选项C,函数的定义域为R,但当x=0时,y=1≠0,故不是奇函数;
选项D,为奇函数,在(-∞,0)和(0,+∞)上均为增函数,但在整个定义域上没有单调性,故不合题意.
故选A
点评:本题为函数的基本性质的判断,熟练掌握函数的性质是解决问题的关键,属基础题.
分析:逐个验证:选项A,满足f(-x)+f(x)=
 +
+ =0,故为奇函数,由复合函数的单调性可知为增函数,故符合要求;选项B非奇非偶;选项C不是奇函数;选项D,在(-∞,0)和(0,+∞)上均为增函数,但在整个定义域上没有单调性.
=0,故为奇函数,由复合函数的单调性可知为增函数,故符合要求;选项B非奇非偶;选项C不是奇函数;选项D,在(-∞,0)和(0,+∞)上均为增函数,但在整个定义域上没有单调性.解答:选项A,定义域为R,且满足f(-x)+f(x)=
 +
+
=ln(x2+1-x2)=ln1=0,故函数为奇函数,
又函数y=
 为增函数,由复合函数的单调性可知,函数为增函数,故符合要求;
为增函数,由复合函数的单调性可知,函数为增函数,故符合要求;选项B,在定义域(1,+∞)为增函数,但非奇非偶,故不合题意;
选项C,函数的定义域为R,但当x=0时,y=1≠0,故不是奇函数;
选项D,为奇函数,在(-∞,0)和(0,+∞)上均为增函数,但在整个定义域上没有单调性,故不合题意.
故选A
点评:本题为函数的基本性质的判断,熟练掌握函数的性质是解决问题的关键,属基础题.

练习册系列答案
相关题目
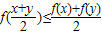 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数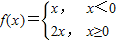
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数