Question

下列命题中正确的是　　　　　.

①如果幂函数的图象不过原点，则或

②定义域为的函数一定可以表示成一个奇函数与一个偶函数的和

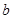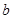③已知直线、、两两异面，则与、、同时相交的直线有无数条

④方程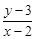＝表示经过点、的直线

⑤方程－＝1表示的曲线不可能是椭圆

 

Answer 1

【答案】

①②③

【解析】

试题分析：对①，要幂函数的图象不过原点，则，解得

或.故正确.

对②，定义域为的函数一定可以表示成一个奇函数与一个偶函数的和,正确.

对③，已知直线、、两两异面，则与、、同时相交的直线有无数条，正确.

对④，方程＝表示经过点、的直线（不含、两点）.错误.

对⑤，设方程－＝1表示的曲线是椭圆，则，解得，故当时，方程－＝1表示的曲线是椭圆，错误.

故正确的是①②③

考点：幂函数，函数的奇偶性，直线与直线的关系，两点式直线方程,椭圆的方程.数形结合思想，转化能力.

点评： 这类问题求解，首先要弄清定义在何时成立，本题中的①③④⑤是最容易出错的.