题目内容
某校从6名教师中,选派4名同时到3个边远地区支教,每个地区至少选派1名.
(Ⅰ) 共有多少种不同的选派方法？
(Ⅱ) 若6名教师中的甲,乙二位教师不能同时支教，共有多少种不同的选派方法？
【答案】
(Ⅰ)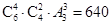 
种
(Ⅱ) 
+
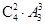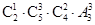=756种
【解析】本试题主要是考查了排列组合的运用。
（1）先确定4名人选，然后从中分组分配，利用分步计数乘法原理表示出即可。
（2）分为两种情况，如果甲,乙二位教师都不支教，有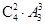种不同的选派方法
或者甲,乙二位教师恰有一名支教，有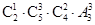种不同的选派方法，然后借助于分类加法计数原理得到。
解：(Ⅰ) 从6名教师中选出4人，有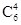
种方法，4名教师选派到3个边远地区支教,每个地区至少选派1名，有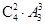种方法，根据分步计数原理，共有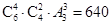种方法．
(Ⅱ) 甲,乙二位教师都不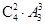支教，有种不同的选派方法
；甲,乙二位教师恰有一名支教，有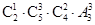种不同的选派方法. 根据分步计数原理，共有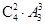+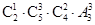=756种方法
练习册系列答案
相关题目
某校从8名教师中选派4名教师同时去4个边远地区支教（每地1人），其中甲和乙不同去，甲和丙只能同去或同不去，则不同的选派方案共有（ ）种．
| A、150 | B、300 | C、600 | D、900 |