题目内容
设数列{an}是首项为4,公差为1的等差数列,Sn为数列{bn}的前n项和,且Sn=n2+2n.(1)求{an}及{bn}的通项公式an和bn,
(2)若f(n)= 问是否存在k∈N*使f(k+27)=4f(k)成立?若存在,求出k的值;若不存在,请说明理由;
问是否存在k∈N*使f(k+27)=4f(k)成立?若存在,求出k的值;若不存在,请说明理由;
(3)若对任意的正整数n,不等式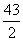 ≤0恒成立,求正数a的取值范围.
≤0恒成立,求正数a的取值范围.
解:(1)an=a1+(n-1)d=4+n-1=n+3.
当n=1时,b1=S1=3.当n≥2时,bn=Sn-Sn-1=n2+2n-(n-1)2-2(n-1)=2n+1.当n=1时上式也成立,∴bn=2n+1(n∈N*).∴an=n+3,bn=2n+1.
(2)假设符合条件的k(k∈N*)存在.由于f(n)=
∴当k为正奇数时,k+27为正偶数.由f(k+27)=4f(k),得2(k+27)+1=4(k+3).∴2k=43,k=![]() (舍去).
(舍去).
当k为正偶数时,k+27为正奇数,由f(k+27)=4f(k),得(k+27)+3=4(2k+1),即7k=26.∴k=![]() (舍去).因此,符合条件的正整数k不存在.
(舍去).因此,符合条件的正整数k不存在.
(3)将不等式变形并把an+1=n+4代入,得a≤![]() .
.
设g(n)=![]() .
.
∴g(n+1)=![]() .
.
∴![]() =
=![]() .
.
又∵![]() ,∴
,∴![]() >1,即g(n+1)>g(n).
>1,即g(n+1)>g(n).
∴g(n)随n的增大而增大.故g(n)min=g(1)=![]() (1+
(1+![]() )=
)=![]() .∴0<a≤
.∴0<a≤![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
设数列{an}是首项为1公比为3的等比数列,把{an}中的每一项都减去2后,得到一个新数列{bn},{bn}的前n项和为Sn,对任意的n∈N*,下列结论正确的是( )
A、bn+1=3bn,且Sn=
| ||
B、bn+1=3bn-2,且Sn=
| ||
C、bn+1=3bn+4,且Sn=
| ||
D、bn+1=3bn-4,且Sn=
|