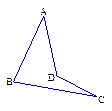
题目内容
(本小题满分12分)
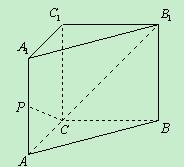
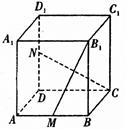
直三棱柱ABO-A1B1O1中,∠AOB=90°,D为AB的中点,AO=BO=BB1=2.
①求证:BO1⊥AB1;
②求证:BO1∥平面OA1D;
③求三棱锥B—A1OD的体积。
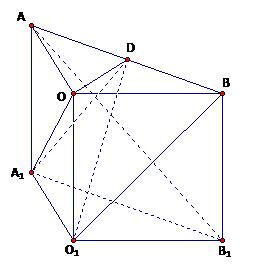
直三棱柱ABO-A1B1O1中,∠AOB=90°,D为AB的中点,AO=BO=BB1=2.
①求证:BO1⊥AB1;
②求证:BO1∥平面OA1D;
③求三棱锥B—A1OD的体积。

①略
②略
③V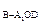 =
=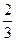
②略
③V
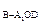 =
=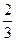
证法1:①连结OB , ∵OO
, ∵OO ⊥平面AOB,∴OO
⊥平面AOB,∴OO ⊥AO
⊥AO
即AO⊥OO ,又AO⊥OB
,又AO⊥OB
∴AO⊥平面OO B
B B
B
∴O B 为A B
为A B 在平面OO
在平面OO B
B B内的射影
B内的射影
又OB="B" B ∴四边形OO
∴四边形OO B
B B为正方形
B为正方形
∴B O ⊥OB
⊥OB
∴B O ⊥A B
⊥A B (三垂线定理)分
(三垂线定理)分
②连结A O 交OA
交OA 于E,再连结DE.
于E,再连结DE.
∵四边形AA O
O O为矩形 ,∴E为A O
O为矩形 ,∴E为A O 的中点.
的中点.
又D为AB的中点,∴BO ∥D……………6分
∥D……………6分
又DE 平面OA
平面OA D,BO
D,BO
 平面OA
平面OA D
D
∴BO ∥平面OA
∥平面OA D
D
③∵V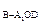 = V
= V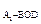 ,
,
又∵AA1⊥平面ABO,∴V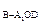 =
=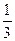 ·S
·S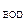 ·A
·A A。
A。
又S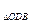 =
=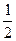 ·S
·S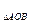 =1,A1A=2,
=1,A1A=2,
∴V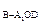 =
=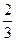 。
。
证法2:以O 为原点建立如图所示的空间直角坐标系,则:
为原点建立如图所示的空间直角坐标系,则:
O (0,0,0),A
(0,0,0),A (2,0,0),B
(2,0,0),B (0,2,0),A(2,0,2),
(0,2,0),A(2,0,2),
B(0,2,2), O(0,0,2), D(1,1,2).
①∵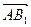 =(-2,2,-2),
=(-2,2,-2),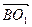 =(0,-2,-2)
=(0,-2,-2)
∴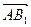 ·
·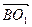 ="(-2)" ·0+2·(-2)+(-2) ·(-2)=0
="(-2)" ·0+2·(-2)+(-2) ·(-2)=0
∴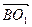 ⊥
⊥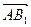 ∴B O
∴B O ⊥A B
⊥A B
②取OA 的中点为E,则E点的坐标是(1,0,1),∴
的中点为E,则E点的坐标是(1,0,1),∴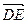 ="(0,-1,-1), " 又
="(0,-1,-1), " 又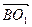 =(0,-2,-2)
=(0,-2,-2)
∴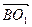 =2
=2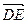 又BO
又BO 、DE不共线, ∴BO
、DE不共线, ∴BO ∥DE
∥DE
又DE 平面OA
平面OA D,BO
D,BO
 平面OA
平面OA D ∴BO
D ∴BO ∥平面OA
∥平面OA D③与证法1相同
D③与证法1相同
 , ∵OO
, ∵OO ⊥平面AOB,∴OO
⊥平面AOB,∴OO ⊥AO
⊥AO即AO⊥OO
 ,又AO⊥OB
,又AO⊥OB ∴AO⊥平面OO
 B
B B
B∴O B
 为A B
为A B 在平面OO
在平面OO B
B B内的射影
B内的射影又OB="B" B
 ∴四边形OO
∴四边形OO B
B B为正方形
B为正方形∴B O
 ⊥OB
⊥OB
∴B O
 ⊥A B
⊥A B (三垂线定理)分
(三垂线定理)分②连结A O
 交OA
交OA 于E,再连结DE.
于E,再连结DE.∵四边形AA
 O
O O为矩形 ,∴E为A O
O为矩形 ,∴E为A O 的中点.
的中点.又D为AB的中点,∴BO
 ∥D……………6分
∥D……………6分又DE
 平面OA
平面OA D,BO
D,BO
 平面OA
平面OA D
D∴BO
 ∥平面OA
∥平面OA D
D③∵V
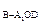 = V
= V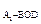 ,
,又∵AA1⊥平面ABO,∴V
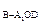 =
=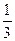 ·S
·S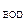 ·A
·A A。
A。又S
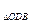 =
=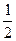 ·S
·S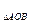 =1,A1A=2,
=1,A1A=2,∴V
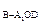 =
=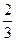 。
。证法2:以O
 为原点建立如图所示的空间直角坐标系,则:
为原点建立如图所示的空间直角坐标系,则:O
 (0,0,0),A
(0,0,0),A (2,0,0),B
(2,0,0),B (0,2,0),A(2,0,2),
(0,2,0),A(2,0,2),B(0,2,2), O(0,0,2), D(1,1,2).
①∵
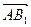 =(-2,2,-2),
=(-2,2,-2),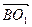 =(0,-2,-2)
=(0,-2,-2)∴
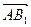 ·
·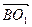 ="(-2)" ·0+2·(-2)+(-2) ·(-2)=0
="(-2)" ·0+2·(-2)+(-2) ·(-2)=0∴
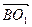 ⊥
⊥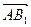 ∴B O
∴B O ⊥A B
⊥A B
②取OA
 的中点为E,则E点的坐标是(1,0,1),∴
的中点为E,则E点的坐标是(1,0,1),∴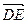 ="(0,-1,-1), " 又
="(0,-1,-1), " 又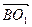 =(0,-2,-2)
=(0,-2,-2)∴
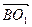 =2
=2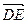 又BO
又BO 、DE不共线, ∴BO
、DE不共线, ∴BO ∥DE
∥DE又DE
 平面OA
平面OA D,BO
D,BO
 平面OA
平面OA D ∴BO
D ∴BO ∥平面OA
∥平面OA D③与证法1相同
D③与证法1相同
练习册系列答案
相关题目
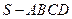 的底面是边长为
的底面是边长为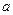 的正方形,且
的正方形,且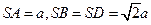 。
。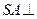 平面
平面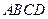 ;
;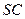 为四棱锥中最长的侧棱,点
为四棱锥中最长的侧棱,点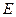 为
为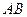 的中点.求直线SE.与平面SAC所成角的正弦值。
的中点.求直线SE.与平面SAC所成角的正弦值。
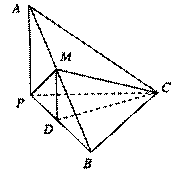
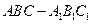 中,
中,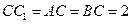 ,
,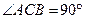 .
.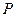 是
是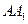 的中点,求四棱锥
的中点,求四棱锥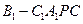 的体积.
的体积.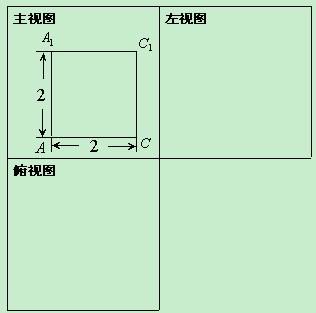
 、
、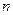 与平面
与平面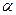 、
、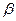 ,有下列四个命题:
,有下列四个命题: 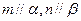 且
且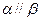 ,则
,则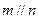 ; ②
; ②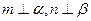 且
且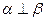 ,则
,则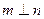 ;
;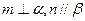 且
且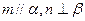 且
且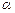 ,直线
,直线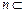 平面
平面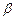 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )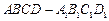 中,
中,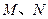 分别为
分别为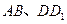 的中点,则异面直线
的中点,则异面直线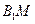 与
与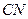 所成角是 ( )
所成角是 ( )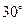
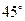
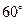
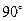
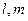 是两条不同的直线,
是两条不同的直线,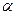 是一个平面,则下列命题错误的是 .
是一个平面,则下列命题错误的是 .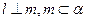 ,则
,则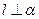 ;②若
;②若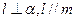 ,则
,则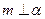 ;
;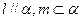 ,则
,则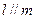 ;④若
;④若 ,则
,则