Question

选修4-1：几何证明选讲

如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连结EC、CD.

（Ⅰ）求证：直线AB是⊙O的切线；

（Ⅱ）若tan∠CED=，⊙O的半径为3，求OA的长.

 

Answer 1

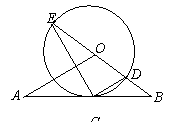解：（Ⅰ）如图，连接OC，∵OA=OB，CA=CB  ∴OC⊥AB

∴AB是⊙O的切线…………4分

（Ⅱ）∵ED是直径，∴∠ECD=90°∴∠E+∠EDC=90°

又∵∠BCD+∠OCD=90°，∠OCD=∠ODC，∴∠BCD=∠E

又∵∠CBD+∠EBC，∴△BCD∽△BEC

∴  ∴BC²=BD•BE

∵tan∠CED=,∴

∵△BCD∽△BEC, ∴…………8分

设BD=x,则BC=2x

又BC²=BD•BE，∴(2x)²=x•(x+6)

解得：x₁=0,x₂=2, ∵BD=x>0, ∴BD=2

∴OA=OB=BD+OD=3+2=5…………10分