题目内容
函数
的最小值、最大值和周期分别是
- A.-1，3，4
- B.-1，1，2
- C.0，3，4
- D.0，1，2
A
分析：由余弦函数的值域，可得函数的最大值为3、最小值为-1．再由三角函数的周期公式算出T=4，从而得到本题的答案．
解答：∵函数的表达式为
∴函数的周期T=
=4，
∵t=
的最大值为1，最小值为-1
∴当x=4k（k∈Z）时，函数的最小值为-1；
当x=4k+2（k∈Z）时，函数的最大值为3
故选：A
点评：本题给出特殊的三角函数式，求函数的最大、最小值和周期，着重考查了三角函数的图象与性质的知识，属于基础题．
分析：由余弦函数的值域，可得函数的最大值为3、最小值为-1．再由三角函数的周期公式算出T=4，从而得到本题的答案．
解答：∵函数的表达式为
∴函数的周期T=
=4，∵t=
的最大值为1，最小值为-1∴当x=4k（k∈Z）时，函数
的最小值为-1；当x=4k+2（k∈Z）时，函数
的最大值为3故选：A
点评：本题给出特殊的三角函数式，求函数的最大、最小值和周期，着重考查了三角函数的图象与性质的知识，属于基础题．
练习册系列答案
相关题目
探究函数
的最小值，并确定取得最小值时x的值.列表如下：
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点，完成以下的问题.
(1)函数
在区间（0，2）上递减，在区间 上递增. 当
时，
.
(2)证明：函数
在区间（0，2）递减.
(3)思考？函数
时有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
的最小值和最大值分别为（ ）
D. －2，
的最小正周期为π.
，求函数g(x)在区间
上的最小值和最大值．
时，求函数
的最小值和最大值；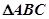
的内角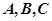
的对应边分别为
，且
，若向量
与向量
共线，求
的值．
的最小值和最大值分别为（
）
B．
C．
D．