题目内容

数列{an}的前n项和为Sn=1-an(n∈N*).

(1)判断数列{an}是否为等差或等比数列;

(2)求数列{an}的前n项和Sn.

解:(1)由an=Sn-Sn-1(n≥2)得an=(1-an)-(1-an-1),

∴an=an-1.∴(n∈N*,n≥2).

∴数列{an}是首项为,公比为的等比数列.∴an=·()n-1.

(2)方法一:利用等比数列前n项和公式Sn=

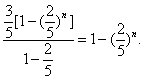
方法二:利用已知条件Sn=1-an=1-·()n-1=1-()n.

练习册系列答案
相关题目
设等比数列{an}的公比q≠1，Sn表示数列{an}的前n项的和，Tn表示数列{an}的前n项的乘积，Tn（k）表示{an}的前n项中除去第k项后剩余的n-1项的乘积，即Tn（k）=
Tn
ak
（n，k∈N+，k≤n），则数列
SnTn
Tn(1)+Tn(2)+…+Tn(n)
的前n项的和是
a12
2-q-q-1
（n+nq-
q-qn+1+1-q1-n
1-q
）
a12
2-q-q-1
（n+nq-
q-qn+1+1-q1-n
1-q
）
（用a1和q表示）
若数列{an}的通项an=
1
pn-q
，实数p，q满足p＞q＞0且p＞1，sn为数列{an}的前n项和．
（1）求证：当n≥2时，pan＜an-1；
（2）求证sn＜
p
(p-1)(p-q)
(1-
1
pn
)；
（3）若an=
1
(2n-1)(2n+1-1)
，求证sn＜
2
3
．
已知Sn是数列{an}的前n项和，an＞0，Sn=
a
2
n
+an
2
，n∈N*，
（1）求证：{an}是等差数列；
（2）若数列{bn}满足b1=2，bn+1=2an+bn，求数列{bn}的通项公式bn．
（2012•商丘二模）数列{an}的前n项和为Sn，若数列{an}的各项按如下规律排列：
1
2
，
1
3
，
2
3
，
1
4
，
2
4
，
3
4
，
1
5
，
2
5
，
3
5
，
4
5
…，
1
n
，
2
n
，…，
n-1
n
，…有如下运算和结论：
①a24=
3
8
；
②数列a1，a2+a3，a4+a5+a6，a7+a8+a9+a10，…是等比数列；
③数列a1，a2+a3，a4+a5+a6，a7+a8+a9+a10，…的前n项和为Tn=
n2+n
4
；
④若存在正整数k，使Sk＜10，Sk+1≥10，则ak=
5
7
．
其中正确的结论是
①③④
①③④
．（将你认为正确的结论序号都填上）
给出下列命题：
①若数列{an}的前n项和Sn=2n+1，则数列{an}为等比数列；
②在△ABC中，如果A=60°，a=
6
，b=4，那么满足条件的△ABC有两解；
③设函数f（x）=x|x-a|+b，则函数f（x）为奇函数的充要条件是a2+b2=0；
④设直线系M：xcosθ+（y-2）sinθ=1（0≤θ≤2π），则M中的直线所能围成的正三角形面积都相等．
其中真命题的序号是
③
③
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网