Question

在正方体ABCD—A₁B₁C₁D₁中，E、F、M分别为AA₁、C₁D₁、BC的中点，那么直线B₁E与FM所成角的余弦值为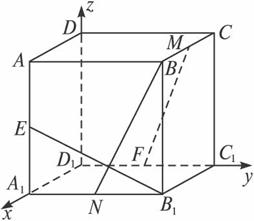

A.0                  B.1                  C.                   D.

Answer 1

答案： A  方法一：建立如图所示的坐标系，不妨设棱长为2，则B₁(2,2,0)、E(2,0,1)、F(0，1，0)、M(1，2，2).=(1，1，2)，=(0,-2,1).

cos〈〉=.

方法二：设A₁B₁的中点为N，FM在面A₁B₁BA上的射影为BN，∵BN⊥B₁E，

∴B₁E⊥MF.∴所成角为90°，余弦值为0.