题目内容
若动点P，Q分别在曲线
和直线2x+y=0上运动，则线段PQ长的最小值为 ．
【答案】分析：根据图形的对称性，只须考虑曲线在第一象限的切线，如图，设与直线2x+y=0平行且在第一象限与曲线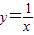
相切的直线方程为：y=-2x+b，切点为A（m，n），只须求出它到直线2x+y=0的距离线段PQ长的最小值．
解答：
解：如图，设与直线2x+y=0平行且在第一象限与曲线
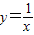相切的直线方程为：y=-2x+b，切点为A（m，n），
∵
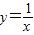，∴y′=-
，
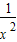根据切线的几何意义得：-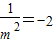
⇒m=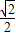
∴切点为A（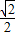
，
），
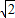它到直线2x+y=0的距离为：d=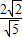
=
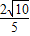
则线段PQ长的最小值为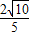
故答案为：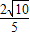
．
点评：本题考查利用导数研究曲线上某点切线方程，点到直线的距离公式的应用，注意线段PQ 取最小值时的条件．
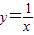相切的直线方程为：y=-2x+b，切点为A（m，n），只须求出它到直线2x+y=0的距离线段PQ长的最小值．解答：
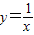解：如图，设与直线2x+y=0平行且在第一象限与曲线相切的直线方程为：y=-2x+b，切点为A（m，n），∵
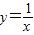，∴y′=-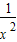，根据切线的几何意义得：-
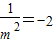⇒m=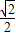∴切点为A（
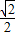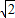，），它到直线2x+y=0的距离为：d=
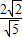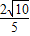
=则线段PQ长的最小值为
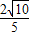
故答案为：
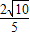．点评：本题考查利用导数研究曲线上某点切线方程，点到直线的距离公式的应用，注意线段PQ 取最小值时的条件．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
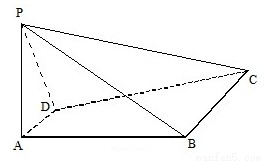
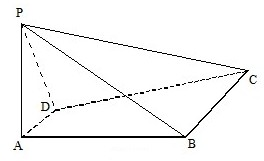如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是直角梯形，其中DA⊥AB，AD∥BC．PA=2AD=BC=2AB=2
．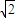