题目内容
(本题满分10分)在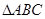 中,已知角
中,已知角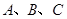 所对的边分别是
所对的边分别是 ,边
,边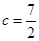 ,且
,且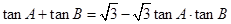 ,又
,又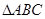 的面积为
的面积为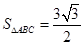 ,求
,求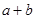 的值.
的值.
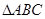 中,已知角
中,已知角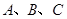 所对的边分别是
所对的边分别是 ,边
,边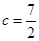 ,且
,且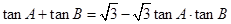 ,又
,又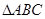 的面积为
的面积为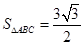 ,求
,求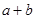 的值.
的值.a+b= 。
。
 。
。本试题主要是考查了解三角形和两角和差公式的综合运用。
先根据已知化简得到tan(A+B)= ,所以C=
,所以C= ,然后利用正弦面积公式得到△ABC的面积为S△ABC=
,然后利用正弦面积公式得到△ABC的面积为S△ABC= ,∴
,∴ absinC=
absinC= 即
即 ab×
ab× =
= ,得到ab=6,再结合余弦定理得到a+b=
,得到ab=6,再结合余弦定理得到a+b= 。
。
解: =
= ,即tan(A+B)=
,即tan(A+B)=
∴tan(π-C)= , ∴-tanC=
, ∴-tanC= ,∴C=
,∴C=
又△ABC的面积为S△ABC= ,∴
,∴ absinC=
absinC= 即
即 ab×
ab× =
= , ∴ab=6
, ∴ab=6
又由余弦定理可得c2=a2+b2-2abcosC
∴( )2= a2+b2-2abcos
)2= a2+b2-2abcos ∴(
∴( )2= a2+b2+ab=(a+b)2-ab∴(a+b)2=
)2= a2+b2+ab=(a+b)2-ab∴(a+b)2= ,
,
∵a+b>0, ∴a+b=
先根据已知化简得到tan(A+B)=
 ,所以C=
,所以C= ,然后利用正弦面积公式得到△ABC的面积为S△ABC=
,然后利用正弦面积公式得到△ABC的面积为S△ABC= ,∴
,∴ absinC=
absinC= 即
即 ab×
ab× =
= ,得到ab=6,再结合余弦定理得到a+b=
,得到ab=6,再结合余弦定理得到a+b= 。
。解:
 =
= ,即tan(A+B)=
,即tan(A+B)=
∴tan(π-C)=
 , ∴-tanC=
, ∴-tanC= ,∴C=
,∴C=
又△ABC的面积为S△ABC=
 ,∴
,∴ absinC=
absinC= 即
即 ab×
ab× =
= , ∴ab=6
, ∴ab=6又由余弦定理可得c2=a2+b2-2abcosC
∴(
 )2= a2+b2-2abcos
)2= a2+b2-2abcos ∴(
∴( )2= a2+b2+ab=(a+b)2-ab∴(a+b)2=
)2= a2+b2+ab=(a+b)2-ab∴(a+b)2= ,
, ∵a+b>0, ∴a+b=


练习册系列答案
相关题目
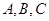 是
是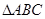 的三个内角,若向量
的三个内角,若向量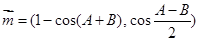 ,
,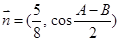 ,且
,且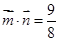 。
。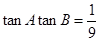 ; (2)求
; (2)求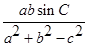 的最大值。
的最大值。 ,则
,则 的值为( )
的值为( )



 ,且
,且 ,则
,则 的值为
的值为  、
、 为锐角,且
为锐角,且 ,
, ,求
,求 的值.
的值.
 )-sin
)-sin =
=  ,则sin(
,则sin( -
- )的值是( )
)的值是( )
 ,
, ,若
,若 ∥
∥ ,则
,则 ( )
( )


 ,
, ,求
,求 的值.
的值.  ,
, ,则
,则 的值为( )
的值为( ) 或
或 
 \
\