题目内容
已知椭圆
＝1上一点P，F1、F2为椭圆的焦点，若∠F1PF2＝
，求△F1PF2的面积．
答案：
解析：
解析：
|
解：如下图，由椭圆第一定义，有|PF1|＋|PF2|＝2a，而在△F1PF2中，由余弦定理有|PF1|2＋|PF2|2－2|PF1|·|PF2|cos ∴(|PF1|＋|PF2|)2－2|PF1|·|PF2|－2|PF1|·|PF2|cos
即4(a2－c2)＝2|PF1|·|PF2|(1＋cos ∴ ＝ |
＝|F1F2|2＝4c2，
＝
|PF1|·|PF2|sin
．
练习册系列答案
相关题目
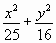＝1上一点P到其一个焦点的距离为3，则点P到另一个焦点的距离为
＝1上一点P与椭圆两焦点
的连线相互垂直，求
的面积．
＝1上一点P到椭圆一个焦点的距离是3，则P点到另一个焦点的距离为：
＝1上一点P，到其左、右两焦点距离之比为1∶3，求点P到两准线的距离及点P的坐标．