题目内容
(任选一题)
(1)已知α、β为实数,给出下列三个论断:
①|α-β|≤|α+β|②|α+β|>5 ③|α|>2
,|β|>2
以其中的两个论断为条件,另一个论断为结论,写出你认为正确的命题是______.
(2)设{an}和{bn}都是公差不为零的等差数列,且
=2,则
的值为______.
(1)已知α、β为实数,给出下列三个论断:
①|α-β|≤|α+β|②|α+β|>5 ③|α|>2
| 2 |
| 2 |
以其中的两个论断为条件,另一个论断为结论,写出你认为正确的命题是______.
(2)设{an}和{bn}都是公差不为零的等差数列,且
| lim |
| n→∞ |
| an |
| bn |
| lim |
| n→∞ |
| b1+b2+…+bn |
| na2n |
(1)由①|α-β|≤|α+β|知,α,β同号,故|α+β|=|α|+|β|,
又由③|α|>2
,|β|>2
可得|α+β|>4
,
又4
≈5.6>5,
所以有|α+β|>5成立,
综上知①③推出②,
故答案为①③?②.
(2)设{an}和{bn}的公差分别为d1 和d2,
∵
=
=
=2,∴d1=2d2.
=
=
=
=
,
故答案为:
.
又由③|α|>2
| 2 |
| 2 |
| 2 |
又4
| 2 |
所以有|α+β|>5成立,
综上知①③推出②,
故答案为①③?②.
(2)设{an}和{bn}的公差分别为d1 和d2,
∵
| lim |
| n→∞ |
| an |
| bn |
| lim |
| n→∞ |
| a1+(n-1)d1 |
| b1+(n-1)d2 |
| d1 |
| d2 |
| lim |
| n→∞ |
| b1+b2+…+bn |
| na2n |
| lim |
| n→∞ |
nb1+
| ||
| n[a1+(2n-1)d1 ] |
| ||
| 2×d1 |
| d2 |
| 4d1 |
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |

练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)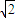 ,|β|>2
,|β|>2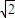
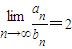 ,则
,则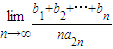 的值为 .
的值为 .