题目内容
如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.(1)求证:MN⊥AB;
(2)若平面PDC与平面ABCD成45°角,求证:平面MND⊥面PDC.
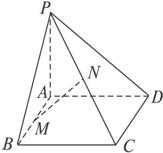
证明:(1)如图,取AC的中点H,连结HN、HM.因为M、N分别是AB、PC的中点,所以MH∥BC,且HN∥PA.

又因为PA⊥面ABCD,所以NH⊥面ABCD.
因为AB⊥BC,即有AB⊥MH,
所以AB⊥MN.
(2)由(1)可得MN⊥CD.
∵PA⊥面ABCD,AD⊥DC,∴∠PDA是二面角PCDA的平面角.由题意∠PDA=45°,即PA=AD.于是Rt△PAM≌Rt△CBM.
∴PM=CM.∴MN⊥PC.
又∵PC∩CD=C,
∴MN⊥面PCD.故平面MND⊥平面PCD.

练习册系列答案
相关题目
 如图,已知PA⊥矩形ABCD所在平面,M、N分别为AB、PC的中点;
如图,已知PA⊥矩形ABCD所在平面,M、N分别为AB、PC的中点;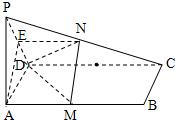 如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB,PC的中点;若P-CD-A为45°的二面角,求证:平面MND⊥平面PDC;
如图,已知PA⊥矩形ABCD所在的平面,M、N分别是AB,PC的中点;若P-CD-A为45°的二面角,求证:平面MND⊥平面PDC; 如图,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.
如图,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.
