题目内容
平面上有![]() 条抛物线,其中每两条都相交于两点,并且每三条都不相交于同一点,则这
条抛物线,其中每两条都相交于两点,并且每三条都不相交于同一点,则这![]() 条抛物线把平面分成多少个部分?
条抛物线把平面分成多少个部分?
![]()
解析:
一条抛物线把平面分成两部分,可记作![]() ,两条抛物线把平面分成的部分比一条抛物线时多了3部分,记作
,两条抛物线把平面分成的部分比一条抛物线时多了3部分,记作![]() ,
,![]() ,
,![]() 条抛物线将平面分成
条抛物线将平面分成![]() 个部分,
个部分,![]() 条抛物线时,由于第
条抛物线时,由于第![]() 条抛物线与前
条抛物线与前![]() 条抛物线共有
条抛物线共有![]() 个交点,这
个交点,这![]() 个交点将第
个交点将第![]() 条抛物线共分成
条抛物线共分成![]() 段,每一段都把原来所在的部分分成了两部分,从而增加了
段,每一段都把原来所在的部分分成了两部分,从而增加了![]() 个部分,就是:
个部分,就是:![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
把以上![]() 个式子相加,得
个式子相加,得![]() .
.

练习册系列答案
相关题目
已知椭圆 ,抛物线
,抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求 ,
, 的标准方程;
的标准方程;
(2)设斜率不为0的动直线 与
与 有且只有一个公共点
有且只有一个公共点 ,且与
,且与 的准线交于
的准线交于 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求出
?若存在,求出 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
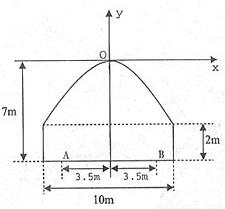
 如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.