题目内容
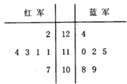 (2013•保定一模)解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.
(2013•保定一模)解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.(1)根据射击数据,计算红、蓝两个小组射击成绩的均值与方差,并说明红军还是蓝军的成绩相对比较稳定;
(2)若从蓝军6名士兵中随机抽取两人,求所抽取的两人的成绩之差不超过2的概率.
分析:(1)记红、蓝两个小组分别为甲,乙,代入公式分别可得其均值和方差由其意义可得结论;
(2)由列举法可得总的基本事件,设A表示“所抽取的两人的成绩之差不超过2”,找出A包含的基本事件,代入古典概型的概率公式可得.
(2)由列举法可得总的基本事件,设A表示“所抽取的两人的成绩之差不超过2”,找出A包含的基本事件,代入古典概型的概率公式可得.
解答:解:(1)记红、蓝两个小组分别为甲,乙,则
=
(107+111+111+113+114+122)=113,
=
(108+109+110+112+115+124)=113,
=
[(107-113)2+2(111-113)2+(113-113)2+(114-113)2+(122-113)2]=2,
=
[(108-113)2+(109-113)2+(110-113)2+(112-113)2+(115-113)2+(124-113)2]=
,
∵
=
,
<
,
∴红组的射击成绩相对比较稳定;
(2)从蓝队6名士兵中随机抽取两人,共有15种不同的取法,
(108,109)(108,110)(108,112)(108,115)(108,124)(109,110)
(109,112)(109,115)(109,124)(110,112)(110,115)(110,124)
(112,115)(112,124)(115,124)
设A表示“所抽取的两人的成绩之差不超过2”,则A包含的基本事件有4种,
(108,109)(108,110),(109,110))(110,112),
故所求的概率为:P(A)=
. |
| x甲 |
| 1 |
| 6 |
. |
| x乙 |
| 1 |
| 6 |
| S | 2 甲 |
| 1 |
| 6 |
| S | 2 乙 |
| 1 |
| 6 |
| 88 |
| 3 |
∵
. |
| x甲 |
. |
| x乙 |
| S | 2 甲 |
| S | 2 乙 |
∴红组的射击成绩相对比较稳定;
(2)从蓝队6名士兵中随机抽取两人,共有15种不同的取法,
(108,109)(108,110)(108,112)(108,115)(108,124)(109,110)
(109,112)(109,115)(109,124)(110,112)(110,115)(110,124)
(112,115)(112,124)(115,124)
设A表示“所抽取的两人的成绩之差不超过2”,则A包含的基本事件有4种,
(108,109)(108,110),(109,110))(110,112),
故所求的概率为:P(A)=
| 4 |
| 15 |
点评:本题考查古典概型及其概率公式,涉及茎叶图和均值方差的应用,属基础题.

练习册系列答案
相关题目
 (2013•保定一模)三棱锥V-ABC的底面ABC为正三角形,侧面VAC垂直于底面,VA=VC,已知其正视图(VAC)的面积为
(2013•保定一模)三棱锥V-ABC的底面ABC为正三角形,侧面VAC垂直于底面,VA=VC,已知其正视图(VAC)的面积为