题目内容
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.(1)求动圆圆心的轨迹M的方程;
(2)设过点P且斜率为
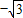 的直线与曲线M相交于A、B两点,求线段AB的长;
的直线与曲线M相交于A、B两点,求线段AB的长;(3)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
【答案】分析:(1)由题意,可知动圆圆心的轨迹为抛物线,从而可求轨迹M的方程;
(2)将直线方程与抛物线方程联立,可求A,B的坐标,从而可求AB长;
(3)假设△ABC能为正三角形,利用 ,导出矛盾,从而得解.
,导出矛盾,从而得解.
解答:解:(1)因为动圆M过定点P(1,0),且与定直线l:x=-1相切
所以由抛物线定义知:圆心M的轨迹是以定点P(1,0)为焦点,定直线l:x=-1为准线的抛物线
所以 圆心M的轨迹方程为y2=4x------(4分)
(2)由题知,直线AB的方程为 ------(6分)
------(6分)
所以 解得:
解得: ------(8分)
------(8分)
∴ ----(10分)
----(10分)
(3)假设△ABC能为正三角形,则设点C的坐标为(-1,y)---(11分)
由题知 (13分)
(13分)
即: ------(14分)
------(14分)
由于上述方程无实数解,因此直线l上不存在这样的点C.------(16分)
点评:本题以抛物线为载体,考查直线与抛物线的位置关系,考查存在性问题,关键是正确理解抛物线的定义.
(2)将直线方程与抛物线方程联立,可求A,B的坐标,从而可求AB长;
(3)假设△ABC能为正三角形,利用
 ,导出矛盾,从而得解.
,导出矛盾,从而得解.解答:解:(1)因为动圆M过定点P(1,0),且与定直线l:x=-1相切
所以由抛物线定义知:圆心M的轨迹是以定点P(1,0)为焦点,定直线l:x=-1为准线的抛物线
所以 圆心M的轨迹方程为y2=4x------(4分)
(2)由题知,直线AB的方程为
 ------(6分)
------(6分)所以
 解得:
解得: ------(8分)
------(8分)∴
 ----(10分)
----(10分)(3)假设△ABC能为正三角形,则设点C的坐标为(-1,y)---(11分)
由题知
 (13分)
(13分)即:
 ------(14分)
------(14分)由于上述方程无实数解,因此直线l上不存在这样的点C.------(16分)
点评:本题以抛物线为载体,考查直线与抛物线的位置关系,考查存在性问题,关键是正确理解抛物线的定义.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.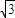 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.