题目内容
(本题满分14分)已知函数 .
.
⑴求函数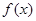 的最小值和最小正周期;
的最小值和最小正周期;
⑵已知 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,
,
若向量 与
与 共线,求
共线,求 的值.
的值.
⑴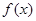 的最小值为
的最小值为 ,最小正周期为
,最小正周期为 .⑵
.⑵ 。
。
解析试题分析:(Ⅰ)

 ------(3分)
------(3分)
∴ 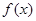 的最小值为
的最小值为 ,最小正周期为
,最小正周期为 . ------(6分)
. ------(6分)
(Ⅱ)∵  , 即
, 即 ∵
∵  ,
, ,∴
,∴  ,∴
,∴  . ------(9分)
. ------(9分)
∵  共线,∴
共线,∴  .
.
由正弦定理  , 得
, 得 ①------(11分)
①------(11分)
∵  ,由余弦定理,得
,由余弦定理,得 , ②
, ②
解方程组①②,得 . ------(14分)
. ------(14分)
考点:二倍角公式;三角函数的周期公式;和差公式;正弦定理;余弦定理;向量共线的条件。
点评:熟记向量平行和垂直的条件,设 :
:
非零向量垂直的充要条件: ;
;
向量共线的充要条件: 。
。

练习册系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
