题目内容
设数列{an}的前n项和为Sn,已知Sn=2an-2n+1(n∈N*).
(1)求数列{an}的通项公式;
(2)令  .用数学归纳法证明:(1-b1)(1-b2)…(1-bn)≥1-(b1+b2+…+bn);
.用数学归纳法证明:(1-b1)(1-b2)…(1-bn)≥1-(b1+b2+…+bn);
(3)设 ,数列{cn}的前n项和为Cn,若存在整数m,使对任意n∈N*且n≥2,都有
,数列{cn}的前n项和为Cn,若存在整数m,使对任意n∈N*且n≥2,都有 成立,求m的最大值.
成立,求m的最大值.
解:(1)由Sn=2an-2n+1,得Sn-1=2an-1-2n(n≥2).
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).
于是 -
-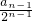 =1,所以数列{
=1,所以数列{  }是公差为1的等差数列.
}是公差为1的等差数列.
又S1=a1=2a1-22,所以a1=4.
所以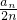 =2+(n-1)=n+1,故an=(n+1)•2n.
=2+(n-1)=n+1,故an=(n+1)•2n.
(2)由(1)知: ,
,
原不等式即证 ≥
≥ .
.
①n=1时,左= =右,故n=1成立;
=右,故n=1成立;
②假设n=k时,
 ,
,
则n=k+1时,

=

> .
.
故n=k+1时,也成立.综合①②知,原不等式恒成立.
(3)因为bn= =log2n2=
=log2n2= ,则B3n-Bn=
,则B3n-Bn= +
+ +
+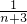 +…+
+…+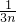 .
.
令f(n)= +
+ +…+
+…+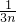 ,
,
则f(n+1)= +
+ +…+
+…+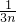 +
+ +
+ +
+ .
.
所以f(n+1)-f(n)= +
+ +
+ -
- =
= +
+ -
- >
> +
+ -
- =0.
=0.
即f(n+1)>f(n),所以数列{f(n)}为递增数列.(7分)
所以当n≥2时,f(n)的最小值为f(2)= +
+ +
+ +
+ =
=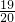 .
.
据题意,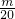 <
<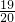 ,即m<19.又m为整数,
,即m<19.又m为整数,
故m的最大值为18.(8分)
分析:(1)根据题中给出的设数列{an}的前n项和为Sn便可求出数列{ }是公差为1的等差数列,将a1=4代入便可求出数列{an}的通项公式;
}是公差为1的等差数列,将a1=4代入便可求出数列{an}的通项公式;
(2)由 ,知原不等式即证
,知原不等式即证 ≥
≥ .由数学归纳法进行证明.
.由数学归纳法进行证明.
(3)先求出数列bn的通项公式,然后求写前n项和Bn的表达式,进而求出的B3n-Bn表达式,然后证明B3n-Bn为递增数列,即当n=2时,B3n-Bn最小,便可求出m的最大值.
点评:本题考查数列的综合应用,具体涉及到通项公式的求法、数学归纳法的证明和最大值的求法.解题时要认真审题,注意合理地进行等价转化.
两式相减,得an=2an-2an-1-2n,即an-2an-1=2n(n≥2).
于是
 -
-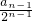 =1,所以数列{
=1,所以数列{  }是公差为1的等差数列.
}是公差为1的等差数列.又S1=a1=2a1-22,所以a1=4.
所以
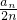 =2+(n-1)=n+1,故an=(n+1)•2n.
=2+(n-1)=n+1,故an=(n+1)•2n.(2)由(1)知:
 ,
,原不等式即证
 ≥
≥ .
.①n=1时,左=
 =右,故n=1成立;
=右,故n=1成立;②假设n=k时,

 ,
,则n=k+1时,


=


>
 .
.故n=k+1时,也成立.综合①②知,原不等式恒成立.
(3)因为bn=
 =log2n2=
=log2n2= ,则B3n-Bn=
,则B3n-Bn= +
+ +
+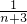 +…+
+…+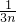 .
.令f(n)=
 +
+ +…+
+…+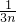 ,
,则f(n+1)=
 +
+ +…+
+…+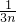 +
+ +
+ +
+ .
.所以f(n+1)-f(n)=
 +
+ +
+ -
- =
= +
+ -
- >
> +
+ -
- =0.
=0.即f(n+1)>f(n),所以数列{f(n)}为递增数列.(7分)
所以当n≥2时,f(n)的最小值为f(2)=
 +
+ +
+ +
+ =
=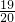 .
.据题意,
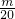 <
<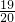 ,即m<19.又m为整数,
,即m<19.又m为整数,故m的最大值为18.(8分)
分析:(1)根据题中给出的设数列{an}的前n项和为Sn便可求出数列{
 }是公差为1的等差数列,将a1=4代入便可求出数列{an}的通项公式;
}是公差为1的等差数列,将a1=4代入便可求出数列{an}的通项公式;(2)由
 ,知原不等式即证
,知原不等式即证 ≥
≥ .由数学归纳法进行证明.
.由数学归纳法进行证明.(3)先求出数列bn的通项公式,然后求写前n项和Bn的表达式,进而求出的B3n-Bn表达式,然后证明B3n-Bn为递增数列,即当n=2时,B3n-Bn最小,便可求出m的最大值.
点评:本题考查数列的综合应用,具体涉及到通项公式的求法、数学归纳法的证明和最大值的求法.解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目