题目内容

6．不等式|3x-1|＞x的解集是（-∞，$\frac{1}{4}$）∪（$\frac{1}{2}$，+∞）．

分析 原不等式等价于3x-1＞x ①，或3x-1＜-x ②，分别求得①②的解集，再取并集，即得所求．

解答 解：原不等式等价于3x-1＞x ①，或3x-1＜-x ②．
解①求得x＞$\frac{1}{2}$，解②求得x＜$\frac{1}{4}$，故不等式|3x-1|＞x的解集是（-∞，$\frac{1}{4}$）∪（$\frac{1}{2}$，+∞），
故答案为：（-∞，$\frac{1}{4}$）∪（$\frac{1}{2}$，+∞）．

点评 本题主要考查绝对值不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．

练习册系列答案
相关题目
16．已知抛物线y2=2px（p＞0）的焦点F到双曲线$\frac{x^2}{a^2}-\frac{y^2}{{3{a^2}}}$=1的渐近线的距离为$\frac{{\sqrt{3}}}{2}$，A，B为抛物线上的两动点，线段AB的中点M在定直线y=2上，则直线AB的斜率为1．
17．2014年第二届夏季青年奥林匹克运动会将在中国南京举行，为了迎接这一盛会，某公司计划推出系列产品，其中一种是写有“青奥吉祥数”的卡片．若设正项数列{an}满足n（n+1）an2-an-1=0，定义使log2ak为整数的实数k为“青奥吉祥数”，则在区间[1，2014]内的所有“青奥吉祥数之和”为2047．
14．已知⊙O：x2+y2=1．若直线y=$\sqrt{k}$x+2上总存在点P，使得过点P的⊙O的两条切线互相垂直，则实数k的最小值为1．
1．已知函数f（x）=$\frac{1}{2}{x^2}$+x，数列{an}满足：a1=1，an+1=f（an）（n∈N*）．
（Ⅰ） 求a2，a3；
（Ⅱ）  证明：an+1＞$\frac{{a}_{n}}{2}$+$\frac{7}{8}$；
（Ⅲ）  求证：$\frac{1}{2}$＜$\frac{1}{2+{a}_{1}}$+$\frac{1}{2+{a}_{2}}$+…+$\frac{1}{2+{a}_{n}}$＜1（n≥2，n∈N*）．
11．椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的长轴长是（　　）
A．2B．3C．4D．6
18．已知sinα-cosα=$\frac{1}{5}$（0＜α＜$\frac{π}{2}$），则sin2α=$\frac{24}{25}$，sin（2α-$\frac{π}{4}$）=$\frac{31\sqrt{2}}{50}$．
15．已知命题：
①如果对于任意的n∈N*，n2+（a-4）n+3+a≥0恒成立，则实数a的取值范围是$[{\frac{1}{3}，+∞}）$；
②命题“?x∈R，x2+x+1＜0”的否定是“?x∈R，x2+x+1＜0”；
③在△ABC中，sinA＞sinB的充要条件是A＞B；
④函数$f（x）=sin（{2x+\frac{π}{3}}）$在$[{0，\frac{π}{6}}]$上为增函数．
以上命题中正确的是①（填写所有正确命题的序号）．
16．执行如图所示的程序框图，若a=7．则输出的S=（　　）
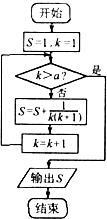
A．$\frac{6}{7}$B．$\frac{15}{8}$C．$\frac{13}{7}$D．$\frac{11}{6}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网