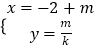题目内容
【题目】已知数列{an}的前n项和Sn=﹣ 
n2+kn（其中k∈N+），且Sn的最大值为8．
（1）确定常数k，求an；
（2）求数列 
的前n项和Tn ．
【答案】
（1）解：当n=k时， 
取得最大值
即 
= 
k2=8
∴k=4，Sn=﹣ n2+4n
从而an=sn﹣sn﹣1= 
﹣[﹣ （n﹣1）2+4（n﹣1）]= 
又∵ 
适合上式
∴ 
（2）解：∵ 
= 
∴ 
两式相减可得， 
= 
= 
∴ 
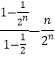【解析】（1）由二次函数的性质可知，当n=k时， 取得最大值，代入可求k，然后利用an=sn﹣sn﹣1可求通项（2）由 = ，可利用错位相减求和即可
【考点精析】本题主要考查了等差数列的通项公式（及其变式）和数列的前n项和的相关知识点，需要掌握通项公式：
或
；数列{an}的前n项和sn与通项an的关系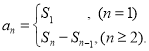
才能正确解答此题．
练习册系列答案
相关题目
