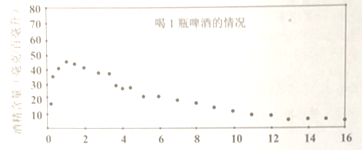
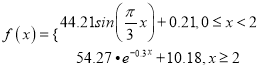题目内容
【题目】已知函数![]() .
.
(1)证明函数![]() 在
在![]() 上为减函数;
上为减函数;
(2)求函数![]() 的定义域,并求其奇偶性;
的定义域,并求其奇偶性;
(3)若存在![]() ,使得不等式
,使得不等式![]() 能成立,试求实数a的取值范围.
能成立,试求实数a的取值范围.
【答案】(1)证明见解析;(2)![]() ,奇函数;(3)
,奇函数;(3)![]() .
.
【解析】
(1)利用单调性定义证明即可.
(2)根据条件可得![]() ,其解集即为函数的定义域,可判断定义域关于原点对称,再根据奇偶性定义可判断函数的奇偶性.
,其解集即为函数的定义域,可判断定义域关于原点对称,再根据奇偶性定义可判断函数的奇偶性.
(3)令![]() ,考虑
,考虑![]() 在
在![]() 上有解即可,参变分离后利用基本不等式可求实数
上有解即可,参变分离后利用基本不等式可求实数![]() 的取值范围.
的取值范围.
(1)![]() ,
,![]() ,
,![]() ,
,
又 ,
,
因为![]() ,
,![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,![]() ,
,
故![]() 即
即![]() ,所以函数
,所以函数![]() 在
在![]() 上为减函数.
上为减函数.
(2)![]() 的
的![]() 满足的不等关系有:
满足的不等关系有:![]() 即
即![]() ,
,
故![]() ,解得
,解得![]() ,
,
故函数的定义域为![]() ,
,![]() ,该定义域关于原点对称.
,该定义域关于原点对称.
令![]()
又![]()
![]() ,
,
故![]() 为奇函数.
为奇函数.
(3)令![]() ,因为
,因为![]() ,故
,故![]() .
.
故在![]() 上不等式
上不等式![]() 能成立即为
能成立即为
存在![]() ,使得
,使得![]() ,所以
,所以![]() 在
在![]() 上能成立,
上能成立,
令![]() ,则
,则![]() 且
且 ,
,
由基本不等式有![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
所以![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
故![]() 的最大值为
的最大值为![]() ,所以a的取值范围为
,所以a的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好