题目内容
一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本。
已知B层中每个个体被抽到的概率都为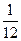 ,则总体中的个体数为 。
,则总体中的个体数为 。
120
解析

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
某中学对高二甲、乙两个同类班级进行加强语文阅读理解训练对提高数学应用题得分率作用的试验,其中甲班为实验班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用试题测试的平均成绩(均取整数)如表所示:
| | 60分以下 | 61﹣70分 | 71﹣80分 | 81﹣90分 | 91﹣100分 |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 3 | 9 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)试分析估计两个班级的优秀率;
(2)由以上统计列出2×2列联表.
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:
| 日期 | 12月 1日 | 12月 2日 | 12月 3日 | 12月 4日 | 12月 5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,
剩下的2组数据用于回归方程检验.
(1)若选取的是12月1日与12月5日的2组数据,
请根据12月2日至12月4日的数据,求出y关于x的线性回归方程
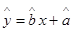 ;
;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(3)请预测温差为14℃的发芽数。
我市某高中的一个综合实践研究小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差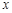 (°C) (°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 (个) (个) | 22 | 25 | 29 | 26 | 16 | 12 |
该综合实践研究小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出
 关于
关于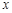 的线性回归方程
的线性回归方程 .
.(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
参考数据:
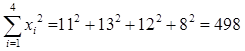 ;
;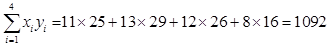 .
.  的估计值.
的估计值.
 的抽样比用分层抽样的方法抽取样本,则应抽取高一学生数为
的抽样比用分层抽样的方法抽取样本,则应抽取高一学生数为  名、
名、 名、
名、 名,若高三学生共抽取
名,若高三学生共抽取 名,则高一年级每一位学生被抽到的概率是___________.
名,则高一年级每一位学生被抽到的概率是___________.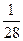 ,则总体中的个体数为 _____ 。
,则总体中的个体数为 _____ 。