题目内容
如图,在底面为直角梯形的四棱锥![]() 中
中![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴求证:![]()
![]() ;
;
⑵求直线![]() 与平面
与平面![]() 所成的角;
所成的角;
⑶设点![]() 在棱
在棱![]() 上,
上,![]() ,若
,若![]() ∥平面
∥平面![]() ,求
,求![]() 的值.
的值.
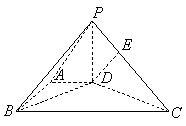
【命题意图】本小题将直四棱锥的底面设计为梯形,考查平面几何的基础知识.同时题目指出一条侧棱与底面垂直,搭建了空间直角坐标系的基本架构.本题通过分层设计,考查了空间平行、垂直,以及线面成角等知识,考查学生的空间想象能力、推理论证能力和运算求解能力.
【试题解析】解:【方法一】(1)证明:由题意知![]() 则
则![]()
![]()
![]() (4分)
(4分)
(2)∵![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() .
.
∴平面![]()
![]() 平面
平面![]() .
.
过![]() 作
作![]() //
//![]() 交
交![]() 于
于![]()
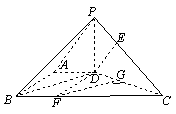
过点![]() 作
作![]()
![]() 交
交![]() 于
于![]() ,则
,则
∠![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
 |  | ||
在Rt△![]() 中,∠
中,∠![]() ,
,![]() ,
,
∴![]() ,∴∠
,∴∠![]() .
.
即直线![]() 与平面
与平面![]() 所成角为
所成角为![]() . (8分)
. (8分)
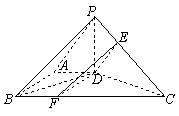
(3)连结![]() ,∵
,∵![]() ∥
∥![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.
又∵![]() ∥平面
∥平面![]() ,
,
∴平面![]() ∥平面
∥平面![]() ,∴
,∴![]() ∥
∥![]() .
.
又∵![]()
∴![]() ∴
∴![]() ,即
,即![]()
(12分)
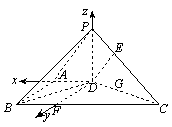
【方法二】如图,在平面ABCD内过D作直线DF//AB,交BC于F,分别以DA、DF、DP所在的直线为x、y、z轴建立空间直角坐标系.
(1)设![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() . (4分)
. (4分)
(2)由(1)知![]() .
.
由条件知A(1,0,0),B(1,![]() ,0),
,0),
![]() .
.
 |
设![]() ,
,
则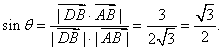
![]() 即直线
即直线![]() 为
为![]() . (8分)
. (8分)
(3)由(2)知C(-3,![]() ,0),记P(0,0,a),则
,0),记P(0,0,a),则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
而![]() ,所以
,所以![]() ,
,
![]()
![]() =
=![]()
设![]() 为平面PAB的法向量,则
为平面PAB的法向量,则 ,即
,即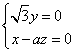 ,即
,即![]() .
.
![]() 进而得
进而得![]() ,
,
由![]() ,得
,得![]() ∴
∴![]()
![]() (12分)
(12分)

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1, 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点. 如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯ABCD,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N分别为PC,PB的中点.
