Question

某食品公司为了解某种新品种食品的市场需求，进行了20天的测试，人为地调控每天产品的单价P（元/件）：前10天每天单价呈直线下降趋势（第10天免费赠送品尝），后10天呈直线上升，其中4天的单价记录如表：
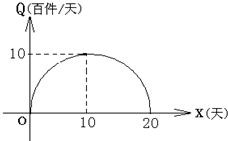
而这20天相应的销售量Q（百件/天）与x对应的点（x，Q）在如图所示的半圆上．
（1）写出每天销售收入y（元）与时间x（天）的函数关系式y=f（x）；
（2）在这20天中哪一天销售收入最高？为使每天销售收入最高，按此次测试结果应将单价P定为多少元为好？（结果精确到1元）

Answer 1

【答案】分析：①前10天每天单价呈直线下降趋势后10天呈直线上升，所以单价是天数的分段函数且两段都是直线，利用两点式写出函数
②销售收入等于单价乘以销售量，将收入表示成时间的函数，利用基本不等式求销售收入最值
解答：解：（1），，x∈[1，20]，x∈N^*，
∴．

（2）∵，
∴当且仅当（x-10）²=100-（x-10）²，
即时，y有最大值．
∵x∈N^*，
∴取x=3或17时，（元），
此时，p=7（元）．
答：第3天或第17天销售收入最高，此时应将单价P定为7元为好．
点评：本题考查将实际问题转化成数学问题，利用基本不等式求最值时，注意等号的取的时自变量是否在定义域内．