题目内容
设函数f(x)=
,g(x)=
,对任意x1、x2∈(0,+∞),不等式
≤
恒成立,则正数k的取值范围是
| e2x2+1 |
| x |
| e2x |
| ex |
| g(x1) |
| k |
| f(x2) |
| k+1 |
k≥1
k≥1
.分析:当x>0时,f(x)=
=e2x+
,利用基本不等式可求f(x)的最小值,对函数g(x)求导,利用导数研究函数的单调性,进而可求g(x)的最大值,由
≤
恒成立且k>0,则
≤
,可求
| e2x2+1 |
| x |
| 1 |
| x |
| g(x1) |
| k |
| f(x2) |
| k+1 |
| g(x)max |
| k |
| f(x)max |
| k+1 |
解答:解:∵当x>0时,f(x)=
=e2x+
≥2
=2e
∴x1∈(0,+∞)时,函数f(x1)有最小值2e
∵g(x)=
∴g′(x)=
=
当x<1时,g′(x)>0,则函数g(x)在(0,1)上单调递增
当x>1时,g′(x)<0,则函数在(1,+∞)上单调递减
∴x=1时,函数g(x)有最大值g(1)=e
则有x1、x2∈(0,+∞),f(x1)min=2e>g(x2)max=e
∵
≤
恒成立且k>0
∴
≤
∴k≥1
故答案为k≥1
| e2x2+1 |
| x |
| 1 |
| x |
e2x•
|
∴x1∈(0,+∞)时,函数f(x1)有最小值2e
∵g(x)=
| e2x |
| ex |
∴g′(x)=
| e2•(ex-xex) |
| e2x |
| e2(1-x) |
| ex |
当x<1时,g′(x)>0,则函数g(x)在(0,1)上单调递增
当x>1时,g′(x)<0,则函数在(1,+∞)上单调递减
∴x=1时,函数g(x)有最大值g(1)=e
则有x1、x2∈(0,+∞),f(x1)min=2e>g(x2)max=e
∵
| g(x1) |
| k |
| f(x2) |
| k+1 |
∴
| e |
| k |
| 2e |
| k+1 |
∴k≥1
故答案为k≥1
点评:本题主要考查了利用基本不等式求解函数的最值,导数在函数的单调性,最值求解中的应用是解答本题的另一重要方法,函数的恒成立问题的转化,本题具有一定的难度

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
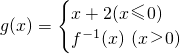 ,则g[g(-1)]=________.
,则g[g(-1)]=________.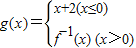 ,则g[g(-1)]= .
,则g[g(-1)]= .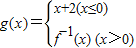 ,则g[g(-1)]= .
,则g[g(-1)]= .