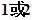题目内容
△ABC的角A、B、C的对边分别为a、b、c, =(2b-c,a),
=(2b-c,a), =(cosA,-cosC),且
=(cosA,-cosC),且 ⊥
⊥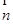 .
.
(Ⅰ)求角A的大小;
(Ⅱ)当y=2sin2B+sin(2B+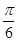 )取最大值时,求角
)取最大值时,求角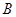 的大小.
的大小.
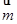 =(2b-c,a),
=(2b-c,a),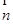 =(cosA,-cosC),且
=(cosA,-cosC),且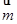 ⊥
⊥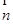 .
.(Ⅰ)求角A的大小;
(Ⅱ)当y=2sin2B+sin(2B+
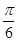 )取最大值时,求角
)取最大值时,求角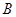 的大小.
的大小. (Ⅰ) A=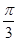 .(Ⅱ) B=
.(Ⅱ) B=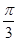 时,y取最大值2.
时,y取最大值2.
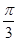 .(Ⅱ) B=
.(Ⅱ) B=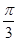 时,y取最大值2.
时,y取最大值2.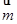 ⊥
⊥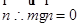 .考查数量积的坐标表示,
.考查数量积的坐标表示,,求y=2sin2B+sin(2B+
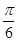 )取最大值时,将函数解析式化为y=1+sin(2B-
)取最大值时,将函数解析式化为y=1+sin(2B-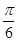 ).
).然后作用的角用整体法-
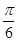 <2B-
<2B-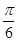 <
<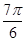 ,在范围内求最值。
,在范围内求最值。解: (Ⅰ)由
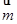 ⊥
⊥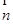 ,得
,得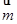 ·
·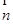 =0,从而(2b-c)cosA-acosC=0,
=0,从而(2b-c)cosA-acosC=0,由正弦定理得2sinBcosA-sinCcosA-sinAcosC=0
∴2sinBcosA-sin(A+C)=0,2sinBcosA-sinB=0,
∵A、B∈(0,π),∴sinB≠0,cosA=
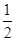 ,故A=
,故A=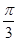 .……………………6分
.……………………6分(Ⅱ)y=2sin2B+2sin(2B+
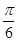 )=(1-cos2B)+sin2Bcos
)=(1-cos2B)+sin2Bcos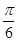 +cos2Bsin
+cos2Bsin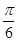
=1+
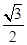 sin2B-
sin2B-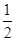 cos2B=1+sin(2B-
cos2B=1+sin(2B-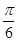 ).
).由(Ⅰ)得,0<B<
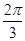 ,-
,-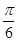 <2B-
<2B-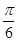 <
<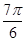 ,
,∴当2B-
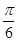 =
=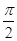 ,即B=
,即B=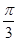 时,y取最大值2
时,y取最大值2
练习册系列答案
相关题目
 的内角
的内角 的对边
的对边 ,
, 。
。 边的长;(2)求角
边的长;(2)求角 的大小; (3)求
的大小; (3)求 的内角A、B、C、所对的边分别为a、b、c,已知
的内角A、B、C、所对的边分别为a、b、c,已知 
 的值.
的值. 中,内角A、B、C依次成等差数列,
中,内角A、B、C依次成等差数列,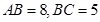 ,则
,则 ,
, ,
, ,那么
,那么 等于_______________
等于_______________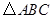 中,
中,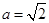 ,
,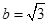 ,
,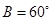 ,那么角
,那么角 等于
等于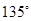
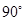
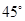
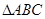 中,
中,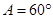 ,
,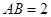 ,且
,且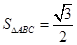 ,则边
,则边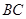 的长为( )
的长为( )
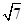
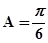 ,
,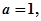 ,
,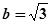 ,则c=( )
,则c=( )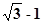 D、
D、