题目内容
已知函数 的图像经过点
的图像经过点 ,
, ,且当
,且当 时,
时, 取得最大值
取得最大值 。
。
①求 的解析式;
的解析式;
②求函数 的单调区间。
的单调区间。
【答案】
(1) (2)函数
(2)函数 的单调递增区间为
的单调递增区间为 函数
函数 的单调递减区间为
的单调递减区间为
【解析】(1)根据图象过两点列出两个方程,再根据三角函数最值得出参数a的值,从而求出函数解析式;(2)利用三角函数单调区间的结论化简即可得到函数的单调区间。
(1)由题意知 ,
,
 …………………2分
…………………2分


当 时,由
时,由 解得
解得 …………………4分
…………………4分
当 时,
时, 无解;…………………5分
无解;…………………5分
当 时,由
时,由 相矛盾,…………………6分
相矛盾,…………………6分
综上可知:
 …………………7分
…………………7分
(2)

 函数
函数 的单调递增区间为
的单调递增区间为 …………………9分
…………………9分


 函数
函数 的单调递减区间为
的单调递减区间为 …………………11分
…………………11分
故函数 的单调递增区间为
的单调递增区间为 函数
函数 的单调递减区间为
的单调递减区间为

练习册系列答案
相关题目
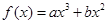 的图像经过点
的图像经过点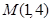 ,曲线在点
,曲线在点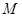 处的切线恰好与直线
处的切线恰好与直线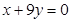 垂直.
垂直.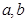 的值;
的值;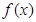 在区间
在区间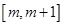 上单调递增,求实数
上单调递增,求实数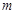 的取值范围.
的取值范围. 的 图像经过点
的 图像经过点 ,
, ,
, 为数列
为数列 的前n项和。
的前n项和。
 及
及
 满足
满足 ,记
,记
 对
对 的取值范围。高☆考♂资♀源?网
的取值范围。高☆考♂资♀源?网