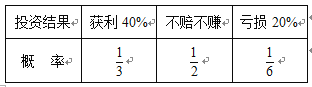
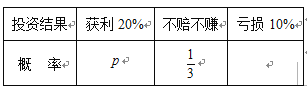
题目内容
【题目】椭圆
的右焦点为
，
为圆
与椭圆
的一个公共点，
.
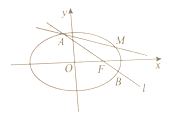
（Ⅰ）求椭圆的标准方程；
（Ⅱ）如图，过
作直线
与椭圆交于
，
两点，点
为点
关于
轴的对称点.
（1）求证：
；
（2）试问过
，的直线是否过定点？若是，请求出该定点；若不是，请说明理由.
【答案】（Ⅰ）
；（Ⅱ）（1）见解析；（2）见解析
【解析】
（Ⅰ）根据题意布列关于a，b的方程组，即可得到椭圆
的标准方程；
（Ⅱ）（1）由题意，设
的方程为
，联立方程可得
，利用韦达定理即可得到结果；（2）直线
的方程为
，可化为
.从而得到定点.
（Ⅰ）解：设
是椭圆的左焦点，连接
，
，
.
∵
，∴
.
∴
.
∴
.∴
.
又∵
，
，∴
.
∴椭圆的标准方程为.
（Ⅱ）（1）证明：① 当直线斜率为0时，的方程为
，∴
，等式
显然成立；
②当直线斜率不为0时，由题意，设的方程为.
∵
，
，点
为点
关于
轴的对称点，则
.
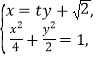整理，得.
，
，
.
∴
.
∴等式成立.
（2）解：过
，的直线过定点.
①当直线斜率不为0时，∵
，
∴直线的方程为，
即
，
即
.
由（1）可知
，
，
∴
.
∴ .
∴过，的直线过定点
；
②当直线斜率为0时，的方程为，直线也过定点.
综上可知，过，的直线过定点.
【题目】“双十一网购狂欢节”源于淘宝商城（天猫）2009年11月11日举办的促销活动，当时参与的商家数量和促销力度均有限，但营业额远超预想的效果，于是11月11日成为天猫举办大规模促销活动的固定日期.如今，中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近8年“双十一”期间的宣传费用
（单位：万元）和利润
（单位：十万元）之间的关系，搜集了相关数据，得到下列表格：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）请用相关系数
说明与之间是否存在线性相关关系（当
时，说明与之间具有线性相关关系）；
（2）建立关于的线性回归方程（系数精确到
），预测当宣传费用为
万元时的利润，
附参考公式：回归方程
中
和
最小二乘估计公式分别为
，
，相关系数
参考数据：
，
，
，
